Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:* Nếu p=2 => p+2=2+2=4 là hợp số (trái với đề bài)
* Nếu p=3 => p+2=3+2=5 là số nguyên tố
=> p+4=3+4=7 là số nguyên tố
=> p=3 thỏa mãn đề bài
* Nếu p là số nguyên tố; p>3 => p có dạng 3k+1 hoặc 3k+2 (k ∈ N*)
* Nếu p=3k+1 => p+2=3k+1+2=3k+3=3(k+1)
Vì 3 ⋮ 3 => 3(k+1) ⋮ 3 => p+2 ⋮ 3, mà p+2 là số nguyên tố lớn hơn 3 => p+2 là hợp số (trái với đề bài)
* Nếu p=3k+2 => p+4=3k+2+4=3k+6=3k+3.2=3(k+2)
Vì 3 ⋮ 3 => 3(k+2) ⋮ 3 => p+4 ⋮ 3, mà p+4 là số nguyên tố lớn hơn 3 => p+4 là hợp số (trái với đề bài)
Vậy p=3 thỏa mãn đề bài

Gọi a, b, c, d là các số nguyên tố. (a>b)
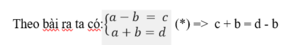
Từ (*) ⇒ a > 2, a là số nguyên tố lẻ ⇒ c + b và d – b là số lẻ. Do b, c, d đều là số nguyên tố nên để c + b và d – b là số lẻ thì ⇒ b chẵn. Vậy b = 2
a. Bài toán đưa về dạng tìm một số nguyên tố a sao cho a – 2 và a + 2 cũng là số nguyên tố.
- Nếu a = 5 ⇒ a – 2 = 3; a + 2 = 7 đều là số nguyên tố
- Nếu a ≠ 5 . Xét 2 trường hợp
+ a chia 3 dư 1 ⇒ a + 2 chia hết cho 3 : không là số nguyên tố
+ a chia 3 dư 2 ⇒ a – 2 chia hết cho 3: không là số nguyên tố
Vậy chỉ có số nguyên tố a duy nhất thoả mãn là 5.
Hai số nguyên tố cần tìm là 5; 2

1) +) Nếu cả hai số nguyên tố đều > 3 => 2 số đó lẻ => tổng và hiệu của chúng là số chẵn => Loại
=> Trong hai số đó có 1 số bằng 2. gọi số còn lại là a
+) Nếu a = 3 : ta có 3 + 2 = 5 ; 3 -2 = 1, 1 không là số nguyên tố => Loại
+) Nếu > 3 thì có thể có dạng: 3k + 1 ( k \(\in\)N*) hoặc 3k + 2 (k \(\in\) N*)
Khi a = 3k + 1 => a+ 2 = 3k + 3 = 3.(k + 1) là hợp số với k \(\in\) N* => Loại
Khi a = 3k + 2 => a + 2 = 3k + 4 ; a - 2 = 3k . 3k; 3k + 4 đều là số nguyên tố với k = 1 . Với k > 1 thì 3k là hợp số nên Loại
Vậy a = 3. 1+ 2 = 5
Vậy chỉ có 2 số 2;5 thỏa mãn

Vì là tổng của 2 số nguyên tố ra số nguyên tố nên tổng phải là số lẻ
Mà lẻ + lẻ = chẳn nên phải có 1 số chẳn
Vậy 1 số là 2
Số còn lại sẽ là số bé nhất có thể
Nếu là 3 thì hiệu sẽ không phải là số nguyên tố
Vậy là số 5
Suy ra 2 SNT đó là 2 và 5
Nếu là số 3 thì

Chỉ ra 2 số nguyên tố mà tổng của. Chúng cũng là 1 số nguyên tố và hiệu củ chúng cũng là 1 số nguyên tố.
-2 số đó là 35 và 6.
Học tốt
Tk me

a) Gọi 2 số đó là : a ; b \(\left(a;b\inℕ^∗\right)\)
Theo bài ra ta có :
\(a+b=162\)( 1 )
\(ƯCLN\left(a,b\right)=18\)( 2 )
\(a=18x;b=18y\left(\left(x,y\right)=1\right)\)( 3 )
Từ ( 1 ) ; ( 2 ) và ( 3 ) suy ra :
\(18x+18y=162\)
\(\Rightarrow18.\left(x+y\right)=162\)
\(\Rightarrow x+y=162:18=9\)
Vì \(\left(x,y\right)=1\)nên :
\(x+y\in\left\{\left(4+5\right);\left(5+4\right);\left(1+8\right);\left(8+1\right);\left(7+2\right);\left(2+7\right)\right\}\)
Vậy \(\left(a;b\right)\in\left\{\left(72;90\right),\left(90;72\right),\left(18;162\right),\left(162;18\right),\left(126;36\right),\left(36;126\right)\right\}\)
b) Nếu \(p=3\Rightarrow p+2=5;p+4=7\)( chọn )
Nếu \(p\)chia cho 3 dư 1 \(\Rightarrow p+2⋮3\)( loại )
Nếu \(p\)chia cho 3 dư 2 \(\Rightarrow p+4⋮3\)( loại )
Vậy \(p=3\)
a) theo cách làm của bạn trên
b) Nếu P=3=> p> p+2=5 ; p+4+7 9 (chọn) Nếu p chia cho 3 dư 1 => p+2 chia hết cho 3; Nếu p chia 3 dư 2=> p+4 chia hết cho 3. Vậy p=3 là hợp lý nhất.
2 và 5
vì 5-2=3(số nguyên tố)
5+2=7(số nguyên tố)
Tick đúng cho mình nha