KC
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 7 2021
Bài 2:
a) Ta có: \(A=\left(7x+5\right)^2+\left(3x-5\right)^2-\left(10-6x\right)\left(5+7x\right)\)
\(=\left(7x+5\right)^2+2\cdot\left(7x+5\right)\cdot\left(3x-5\right)+\left(3x-5\right)^2\)
\(=\left(7x+5+3x-5\right)^2\)
\(=\left(10x\right)^2=100x^2\)
Thay x=-2 vào A, ta được:
\(A=100\cdot\left(-2\right)^2=100\cdot4=400\)
b) Ta có: \(B=\left(2x+y\right)\left(y^2-2xy+4x^2\right)-8x\left(x-1\right)\left(x+1\right)\)
\(=8x^3+y^3-8x\left(x^2-1\right)\)
\(=8x^3+y^3-8x^3+8x\)
\(=8x+y^3\)
Thay x=-2 và y=3 vào B, ta được:
\(B=-2\cdot8+3^3=-16+27=11\)
H9
HT.Phong (9A5)
CTVHS
21 tháng 8 2023
Bài 12:
a) \(\left(\dfrac{1}{2}x+4\right)^2\)
\(=\left(\dfrac{1}{2}x\right)^2+2\cdot\dfrac{1}{2}x\cdot4+4^2\)
\(=\dfrac{1}{4}x^2+4x+16\)
b) \(\left(7x-5y\right)^2\)
\(=\left(7x\right)^2-2\cdot7x\cdot5y+\left(5y\right)^2\)
\(=49x^2-70xy+25y^2\)
c) \(\left(6x^2+y^2\right)\left(y^2-6x^2\right)\)
\(=\left(y^2+6x^2\right)\left(y^2-6x^2\right)\)
\(=y^4-36x^4\)
d) \(\left(x+2y\right)^2\)
\(=x^2+2\cdot x\cdot2y+\left(2y\right)^2\)
\(=x^2+4xy+4y^2\)
e) \(\left(x-3y\right)\left(x+3y\right)\)
\(=x^2-\left(3y\right)^2\)
\(=x^2-9y^2\)
f) \(\left(5-x\right)^2\)
\(=5^2-2\cdot5\cdot x+x^2\)
\(=25-10x+x^2\)
5 tháng 10 2021
Bài 2:
b: Ta có: \(x\left(x+4\right)\left(x-4\right)-\left(x^2+1\right)\left(x^2-1\right)\)
\(=x^3-4x-x^4+1\)
\(=-x^4+x^3-4x+1\)
c: Ta có: \(\left(a+b-c\right)^2-\left(a-c\right)^2-2ab+2ab\)
\(=\left(a+b-c-a+c\right)\left(a+b-c+a-c\right)\)
\(=b\left(2a+b-2c\right)\)
\(=2ab+b^2-2bc\)
28 tháng 7 2023
1:
a: =x^2-7x+49/4-5/4
=(x-7/2)^2-5/4>=-5/4
Dấu = xảy ra khi x=7/2
b: =x^2+x+1/4-13/4
=(x+1/2)^2-13/4>=-13/4
Dấu = xảy ra khi x=-1/2
e: =x^2-x+1/4+3/4=(x-1/2)^2+3/4>=3/4
Dấu = xảy ra khi x=1/2
f: x^2-4x+7
=x^2-4x+4+3
=(x-2)^2+3>=3
Dấu = xảy ra khi x=2
2:
a: A=2x^2+4x+9
=2x^2+4x+2+7
=2(x^2+2x+1)+7
=2(x+1)^2+7>=7
Dấu = xảy ra khi x=-1
b: x^2+2x+4
=x^2+2x+1+3
=(x+1)^2+3>=3
Dấu = xảy ra khi x=-1
AH
Akai Haruma
Giáo viên
28 tháng 12 2018
a)
\(a^2+b^2+2ab+2a+2b+1\)
\(=(a^2+2ab+b^2)+(2a+2b)+1\)
\(=(a+b)^2+2(a+b)+1^2=(a+b+1)^2\)
b)
\(3x(x-2y)+6y(2y-x)\)
\(=3x(x-2y)-6y(x-2y)=(3x-6y)(x-2y)=3(x-2y)(x-2y)\)
\(=3(x-2y)^2\)
AH
Akai Haruma
Giáo viên
28 tháng 12 2018
c)
\(16xy+4y^2-9+16x^2\)
\(=(16x^2+16xy+4y^2)-9\)
\(=(4x+2y)^2-3^2=(4x+2y-3)(4x+2y+3)\)
d)
\(x^4+64y^8=(x^2)^2+(8y^4)^2=(x^2)^2+(8y^4)^2+2.x^2.8y^4-2x^2.8y^4\)
\(=(x^2+8y^4)^2-16x^2y^4=(x^2+8y^4)^2-(4xy^2)^2\)
\(=(x^2+8y^4-4xy^2)(x^2+8y^4+4xy^2)\)
e)
\(3x^2-7x+2=3x^2-6x-x+2=(3x^2-6x)-(x-2)\)
\(=3x(x-2)-(x-2)=(3x-1)(x-2)\)
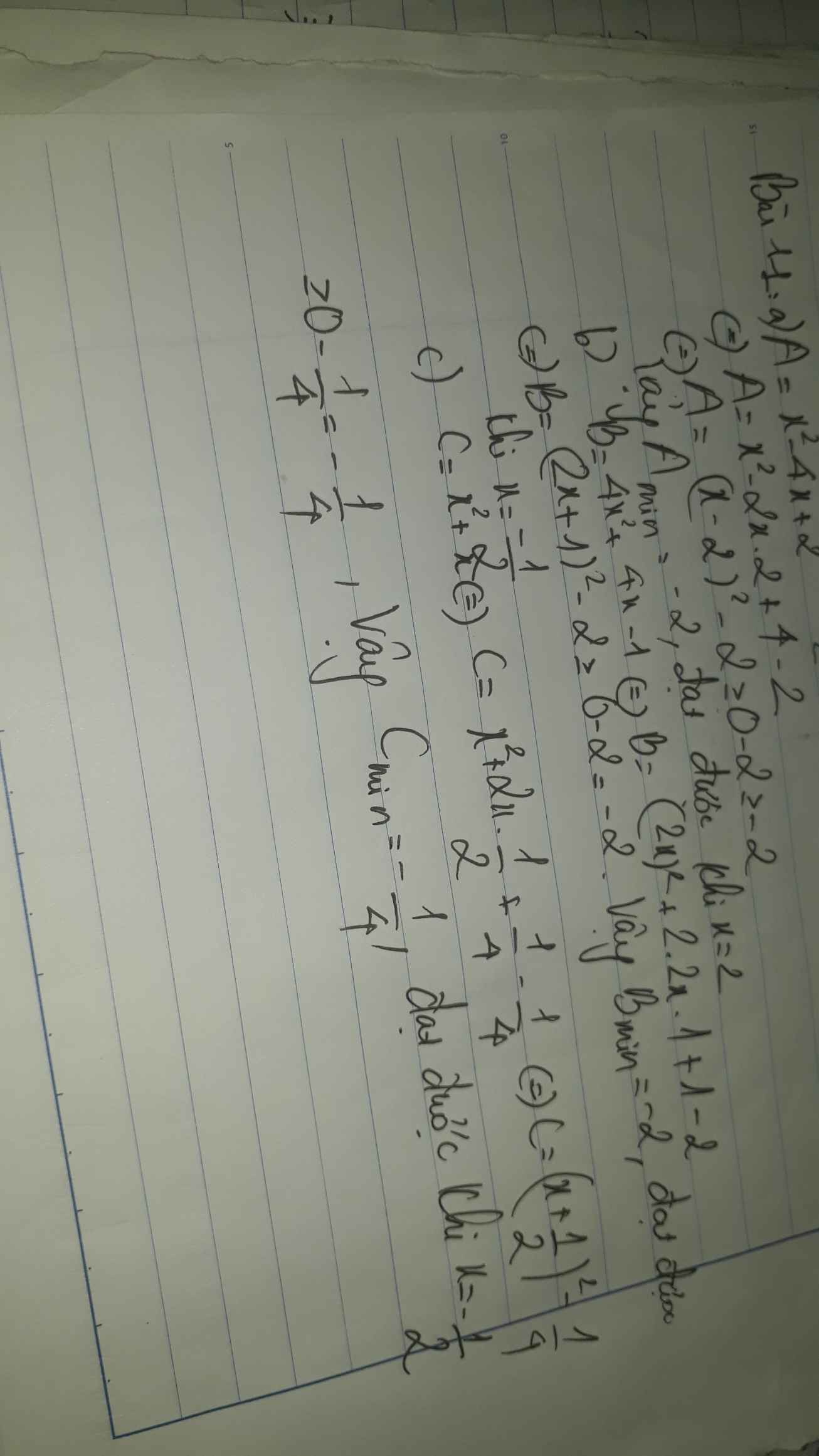
Sorry nhá mk nhầm dấu + nên kq sai :
Ta có : (x + 3)(x - 11) + 2003
= x2 - 8x + 1970
= x2 - 8x + 16 + 1954
= (x - 4)2 + 1954
Mà (x - 4)2 \(\ge0\forall x\)
Nên : (x - 4)2 + 1954 \(\ge1954\forall x\)
Vậy GTNN của biểu thức là : 1954 khi và chỉ khi x = 4
Ta có : (x + 3)(x - 11) + 2003
= x2 - 8x + 33 + 2003
= x2 - 8x + 2026
= x2 - 8x + 16 + 2010
= (x - 4)2 + 2010
Mà (x - 4)2 \(\ge0\forall x\)
Nên : (x - 4)2 + 2010 \(\ge2010\forall x\)
Vậy GTNN của biểu thức là : 2010 khi và chỉ khi x = 4