K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
9 tháng 2 2022
\(x^2+2y^2+2xy+2y+2020\)
\(=\left(x^2+2xy+y^2\right)+\left(y^2+2y+1\right)+2019\)
\(=\left[\left(x+y\right)^2+\left(y+1\right)^2+2019\right]\ge2019\)
Vì \(\left\{{}\begin{matrix}\left(x+y\right)^2\ge0\forall x,y\\\left(y+1\right)^2\ge0\forall y\end{matrix}\right.\)
Dấu "=" \(\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1\end{matrix}\right.\)
NV
0
IM
3 tháng 8 2016
\(A=\left[\left(3x\right)^3-2.2.3x+2^2\right]+6\)
\(A=\left(3x-2\right)^2+6\)
Ta có
\(\left(3x-2\right)^2\ge0\)
\(\left(3x-2\right)^2+6\ge6\)
Dấu " = " xảy ra khi \(3x-2=0\Rightarrow x=\frac{2}{3}\)
Vậy MINA=6 khi x=\(\frac{2}{3}\)
3 tháng 8 2016
\(A=9x^2-12x+10=\left(9x^2-12x+4\right)+6=\left(3x+2\right)^2+6\)
Vì: \(\left(3x+2\right)^2\ge0\) với mọi x
=>\(\left(3x+2\right)^2+6\ge6\)
Vậy GTNN của A là 6 khi \(x=-\frac{2}{3}\)
PA
13 tháng 9 2016
A = 9x2 - 12x + 10
= (3x)2 - 2 . 3x . 2 + 4 + 6
= (3x - 2)2 + 6
(3x - 2)2 lớn hơn hoặc bằng 0
(3x - 2)2 + 6 lớn hơn hoặc bằng 6
Vậy Min A = 6 khi x = 2/3
EC
13 tháng 9 2016
a)\(A=9x^2-12x+10\)
\(A=\left(3x\right)^2-2.2.3x+2^2+6\)
\(A=\left(3x-2\right)^2+6\)
Vì \(\left(3x-2\right)^2\) lớn hơn bằng 0
Suy ra:\(\left(3x-2\right)^2+6\) lớn hơn bằng 6
Dấu = xảy ra khi 3x-2=0
3x=2
x=\(\frac{2}{3}\)
Vậy Min A=6 khi x=\(\frac{2}{3}\)
29 tháng 9 2016
\(A=\left[\left(3x\right)^3-2.2.3x+2^2\right]+6\)
\(=\left(3x-2\right)^2+6\)
Ta có :
\(\left(3x-2\right)^2\ge0\)
\(\Rightarrow\left(3x-2\right)^2+6\ge6\)
Dấu " = " xảy ra khi và chỉ khi \(3x-2=0\)
\(3x=2\)
\(x=\frac{2}{3}\)
Vậy \(Min_A=6\Leftrightarrow x=\frac{2}{3}\)
3 tháng 8 2016
\(A=9x^2-12x+10\)
\(=\left(3x\right)^2-2.2.3x+4+6\)
\(=\left[\left(3x\right)^2-2.2.3x-2^2\right]+6\)
\(=\left(3x-2\right)^2+10\)
Ta có :
\(\left(3x-2\right)^2\ge0\)
\(\Rightarrow\left(3x-2\right)^2+6\ge6\)
\(\Rightarrow A\ge6\)
\(\Rightarrow A_{min}=6\Leftrightarrow3x-2=0\rightarrow x=\frac{2}{3}\)
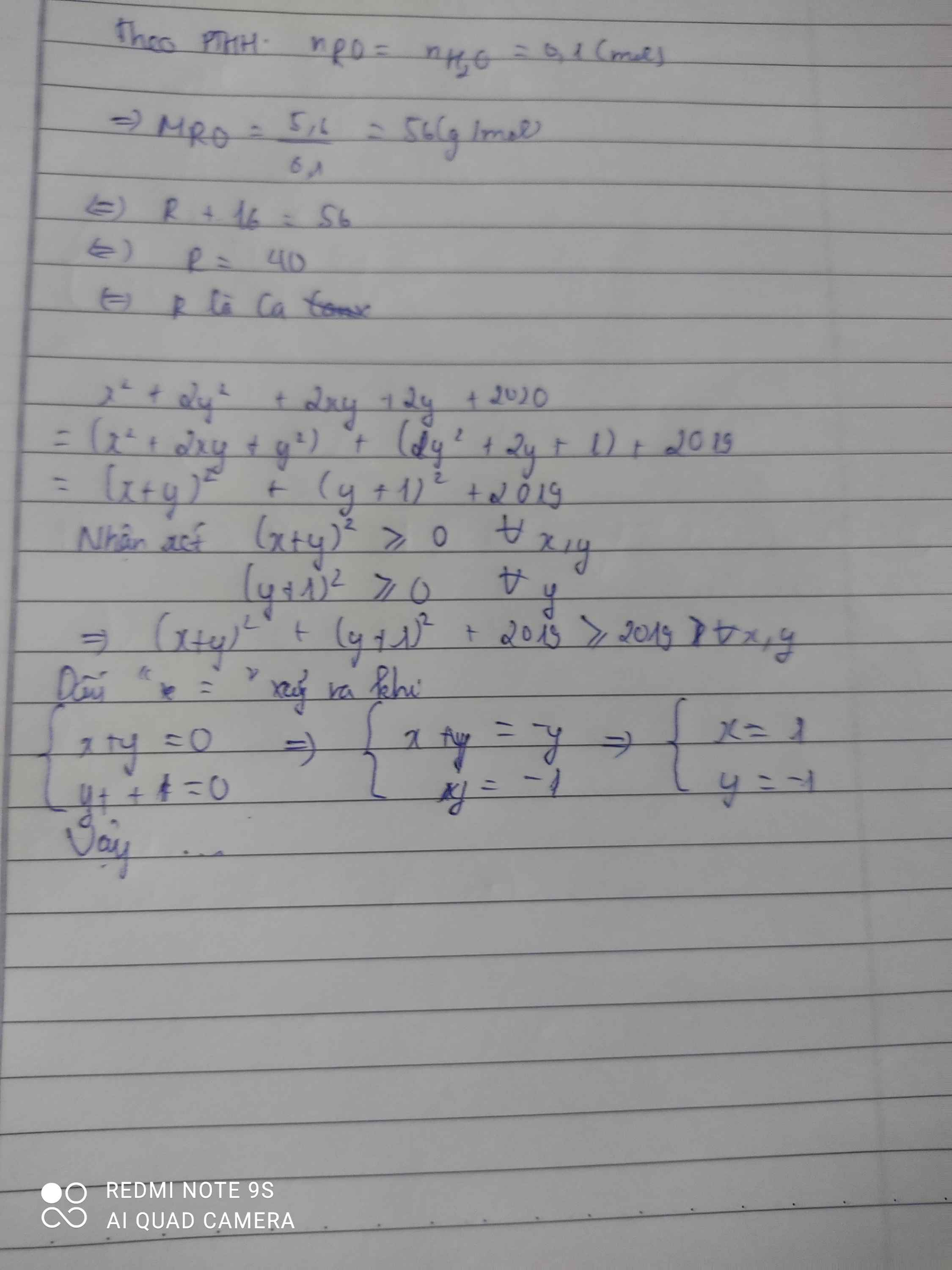
Ta có: x^2 - 12x + 33 = (x^2 - 12x + 36) - 3 = (x - 6)^2 - 3.
Vậy hàm số y = x^2 - 12x + 33 có giá trị nhỏ nhất là -3, khi x = 6.
2. Sử dụng công thức tính đạo hàm:
Đạo hàm của hàm số y = x^2 - 12x + 33 là y' = 2x - 12.
Để tìm giá trị nhỏ nhất, ta giải phương trình y' = 0:
2x - 12 = 0
=> 2x = 12
=> x = 6.
Khi x = 6, ta có y = 6^2 - 12*6 + 33 = -3.
Vậy giá trị nhỏ nhất của hàm số y = x^2 - 12x + 33 là -3, khi x = 6.
\(A=x^2-12x+33\)
\(A=x^2-12x+36-3\)
\(A=\left(x-6\right)^2-3\)
mà \(\left(x-6\right)^2\ge0,\forall x\)
\(\Rightarrow A=\left(x-6\right)^2-3\ge0-3=-3\)
\(\Rightarrow GTNN\left(A\right)=-3\left(x=6\right)\)