K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HH
21 tháng 6 2018
Ta có \(D=d^2+10e^2-6de-10e+26\)
\(D=d^2-6de+\left(3e\right)^2+4e^2-10e+26\)
\(D=\left(d-3e\right)^2+4\left(e^2-\frac{5}{2}e+26\right)\)
\(D=\left(d-3e\right)^2+4\left[e^2-2e.\frac{5}{4}+\left(\frac{5}{4}\right)^2+\frac{391}{16}\right]\)
\(D=\left(d-3e\right)^2+4\left[\left(e-\frac{5}{4}\right)^2+\frac{391}{16}\right]\)
\(D=\left(d-3e\right)^2+4\left(e-\frac{5}{4}\right)^2+\frac{391}{4}\)
Mà \(\left(e-\frac{5}{4}\right)^2\ge0\). Dấu "=" xảy ra khi và chỉ khi \(e=\frac{5}{4}\)
\(\left(d-3e\right)^2\ge0\). Dấu "=" xảy ra khi và chỉ khi \(d-3e=0\)=> \(d=\frac{15}{4}\)
=> \(\left(d-3e\right)^2+\left(e-\frac{5}{4}\right)^2+\frac{391}{4}\ge\frac{391}{4}\). Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}d=\frac{15}{4}\\e=\frac{5}{4}\end{cases}}\)
Vậy GTNN của D là \(\frac{391}{14}\)khi \(\hept{\begin{cases}d=\frac{15}{4}\\e=\frac{5}{4}\end{cases}}\)
25 tháng 10 2017
Con a) Đang nghĩ
b) D = d2 + 10e2 - 6de - 10e + 26
D= d2 - 2.3de + ( 3e)2 + e2 - 2.5e + 52 + 1
D= ( d - 3e)2 + ( e - 5)2 + 1
Do : ( d - 3e)2 lớn hơn hoặc bằng 0 với moi d, e
( e - 5)2 lớn hơn hoặc bằng 0 với mọi e
Vậy : ( d - 3e)2 + 1 lớn hơn hoặc bằng 1 với moi d, e
( e - 5)2 + 1 lớn hơn hoặc bằng 1 với mọi e
Vậy Dmin = 1 khi e = 5 . d = 15
c) E = 4x2 + 12x + 11
E = ( 2x)2 + 2.2x.3 + 32 + 2
E= ( 2x + 3)2 + 2
Do : ( 2x + 3)2 lớn hơn hặc bằng 0 với mọi x
--> ( 2x + 3)2 + 2 lớn hơn hặc bằng 2 với mọi x
Vậy , Emin = 2 KHI VÀ CHỈ KHI \(\dfrac{-3}{2}\)
1 tháng 11 2017
A = 4x4 + 12x2 + 11
A = ( 2x2)2 + 2.2x2.3 + 32 + 2
A = ( 2x + 3)2 + 2
Do : ( 2x + 3)2 lớn hơn hoặc bằng 0 với mọi x
Suy ra : ( 2x + 3)2 + 2 lớn hơn hoặc bằng 2 với mọi x
Vậy , Amin = 2 khi và chỉ khi : 2x + 3 = 0 -> x = \(-\dfrac{3}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 7 2021
\(A=\dfrac{1}{16}c^2-9c+10=\dfrac{1}{16}\left(x-72\right)^2-314\ge-314\)
\(A_{min}=-314\) khi \(c=72\)
\(B=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
\(B_{min}=1\) khi \(\left\{{}\begin{matrix}d=15\\e=5\end{matrix}\right.\)
\(C=4x^4+12x^2+11\)
Do \(\left\{{}\begin{matrix}x^4\ge0\\x^2\ge0\end{matrix}\right.\) ; \(\forall x\Rightarrow C\ge11\)
\(C_{min}=11\) khi \(x=0\)
1 tháng 7 2021
a) Ta có: \(\dfrac{1}{16}c^2-9c+10\)
\(=\left(\dfrac{1}{4}c\right)^2-2\cdot\dfrac{1}{4}c\cdot18+324-314\)
\(=\left(\dfrac{1}{4}c-18\right)^2-314\ge-314\forall c\)
Dấu '=' xảy ra khi \(\dfrac{1}{4}c=18\)
hay c=72
Vậy: Giá trị nhỏ nhất của biểu thức \(\dfrac{1}{16}c^2-9c+10\) là -314 khi c=72
b) Ta có: \(d^2+10e^2-6de-10e+26\)
\(=d^2-6de+9e^2+e^2-10e+25+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\forall d,e\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}e=5\\d=3e=3\cdot5=15\end{matrix}\right.\)
Vậy: Giá trị nhỏ nhất của biểu thức \(d^2+10e^2-6de-10e+26\) là 1 khi e=5 và d=15
c) Ta có: \(4x^4+12x^2+11\)
\(=4x^4+12x^2+9+2\)
\(=\left(2x^2+3\right)^2+2\ge3^2+2=11\)
Dấu '=' xảy ra khi x=0
Vậy: Giá trị nhỏ nhất của biểu thức \(4x^4+12x^2+11\) là 11 khi x=0
DH
2
13 tháng 7 2018
\(A=\frac{1}{16}c^2-9c+10\)
\(A=\left(\frac{1}{16}c^2-9c+324\right)-314\)
\(A=\left(\frac{1}{4}c-18\right)^2-314\)
Mà \(\left(\frac{1}{4}c-18\right)^2\ge0\forall c\)
\(\Rightarrow A\ge-314\)
Dấu "=" xảy ra khi : \(\frac{1}{4}c-18=0\Leftrightarrow c=72\)
Vậy ...
\(B=d^2+10e^2-6de-10e+26\)
\(B=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1\)
\(B=\left(d-3e\right)^2+\left(e-5\right)^2+1\)
Mà \(\left(d-3e\right)^2\ge0\forall d;e\)
\(\left(e-5\right)^2\ge0\forall e\)
\(\Rightarrow B\ge1\)
Dấu "=" xảy ra khi : \(\hept{\begin{cases}d-3e=0\\e-5=0\end{cases}}\Leftrightarrow\hept{\begin{cases}d=15\\e=5\end{cases}}\)
Vậy ...
S
13 tháng 7 2018
a, \(A=\frac{1}{16}c^2-9c+10=\left(\frac{1}{16}c^2-9c+324\right)-314=\left(\frac{1}{4}c-18\right)^2-314\ge-314\)
Dấu "=" xảy ra khi \(\frac{1}{4}c-18=0\Leftrightarrow c=72\)
Vậy Amin = -314 khi c = 72
b, \(B=d^2+10e^2-6de-10e+26\)
\(=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}d-3e=0\\e-5=0\end{cases}\Leftrightarrow\hept{\begin{cases}d-15=0\\e=5\end{cases}\Leftrightarrow}\hept{\begin{cases}d=15\\e=5\end{cases}}}\)
Vậy Bmin = 1 khi d = 15, e = 5
KN
24 tháng 8 2020
1. a. \(A=8a-8a^2+3=-8\left(a-\frac{1}{2}\right)^2+5\)
Vì \(\left(a-\frac{1}{2}\right)^2\ge0\forall a\)\(\Rightarrow-8\left(a-\frac{1}{2}\right)^2+5\le5\)
Dấu "=" xảy ra \(\Leftrightarrow-8\left(a-\frac{1}{2}\right)^2=0\Leftrightarrow a-\frac{1}{2}=0\Leftrightarrow a=\frac{1}{2}\)
Vậy Amax = 5 <=> a = 1/2
b. \(B=b-\frac{9b^2}{25}=-\frac{9}{25}\left(b-\frac{25}{18}\right)^2+\frac{25}{36}\)
Vì \(\left(b-\frac{25}{18}\right)^2\ge0\forall b\)\(\Rightarrow-\frac{9}{25}\left(b-\frac{25}{18}\right)^2+\frac{25}{36}\le\frac{25}{36}\)
Dấu "=" xảy ra \(\Leftrightarrow-\frac{9}{25}\left(b-\frac{25}{18}\right)^2=0\Leftrightarrow b-\frac{25}{18}=0\Leftrightarrow b=\frac{25}{18}\)
Vậy Bmax = 25/36 <=> b = 25/18
F
24 tháng 8 2020
a,\(A=8a-8a^2+3\)
\(=-8\left(a^2-a\right)+3\)
\(=-8\left(a^2-2a\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\right)+3\)
\(=-8\left[\left(a-\frac{1}{2}\right)^2-\frac{1}{4}\right]+3\)
\(=-8\left(a-\frac{1}{2}\right)^2+2+3\)
\(=-8\left(a-\frac{1}{2}\right)^2+5\le5\forall a\)
Dấu"=" xảy ra khi \(\left(a-\frac{1}{2}\right)^2=0\Rightarrow a=\frac{1}{2}\)
Vậy \(Max_A=5\)khi\(a=\frac{1}{2}\)
bài 2:
b,\(D=d^2+10e^2-6de-10e+26\)
\(=d^2-23de+\left(3e\right)^2+e^2-2.5e+5^2+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\forall d,e\)
Dấu"=" xảy ra khi\(\orbr{\begin{cases}\left(d-3e\right)^2=0\\\left(e-5\right)^2=0\end{cases}\Rightarrow\orbr{\begin{cases}d=15\\e=5\end{cases}}}\)
vậy \(D_{min}=1\)khi \(d=15;e=5\)
c,:\(E=4x^4+12x^2+11\)
\(=\left(2x^2\right)^2+2.2x^2.3+3^2+2\)
\(=\left(2x^2+3\right)^2+2\ge2\forall x\)
còn 1 đoạn nx bạn tự lm tiếp,lm giống như D
L
14 tháng 8 2021
a) \(=\left(x+6y\right)\left(x-6y\right)-\left(x-6y\right)\)
\(=\left(x-6y\right)\left(x-6y-1\right)\)
b) \(=x\left(x^2-8x+16\right)\)
\(=x\left(x-4\right)^2\)
c) \(=2\left(x-y\right)^2-18\)
\(=2\left[\left(x-y\right)^2-3^2\right]\)
\(=2\left(x-y+3\right)\left(x-y-3\right)\)
14 tháng 8 2021
a: \(x^2-36y^2-x+6y\)
\(=\left(x-6y\right)\left(x+6y\right)-\left(x-6y\right)\)
\(=\left(x-6y\right)\left(x+6y-1\right)\)
b: \(x^3-8x^2+16x\)
\(=x\left(x^2-8x+16\right)\)
\(=x\left(x-4\right)^2\)
c: \(2x^2-4xy+2y^2-18\)
\(=2\left(x^2-2xy+y^2-9\right)\)
\(=2\left(x-y-3\right)\left(x-y+3\right)\)
d: \(3x^2-7x-10\)
\(=3x^2+3x-10x-10\)
\(=3x\left(x+1\right)-10\left(x+1\right)\)
\(=\left(x+1\right)\left(3x-10\right)\)
14 tháng 8 2021
a: Ta có: \(x^2-36y^2-x+6y\)
\(=\left(x-6y\right)\left(x+6y\right)-\left(x-6y\right)\)
\(=\left(x-6y\right)\left(x+6y-1\right)\)
b: Ta có: \(16x-8x^2+x^3\)
\(=x\left(x^2-8x+16\right)\)
\(=x\left(x-4\right)^2\)
c: Ta có: \(2x^2-4xy+2y^2-18\)
\(=2\left(x^2-2xy+y^2-9\right)\)
\(=2\cdot\left[\left(x-y\right)^2-9\right]\)
\(=2\left(x-y-3\right)\left(x-y+3\right)\)
d: Ta có: \(3x^2-7x-10\)
\(=3x^2+3x-10x-10\)
\(=3x\left(x+1\right)-10\left(x+1\right)\)
\(=\left(x+1\right)\left(3x-10\right)\)
14 tháng 8 2021
e: Ta có: \(x^4-x^2-30\)
\(=x^4-6x^2+5x^2-30\)
\(=x^2\left(x^2-6\right)+5\left(x^2-6\right)\)
\(=\left(x^2-6\right)\left(x^2+5\right)\)
f: Ta có: \(x^2-xy-2y^2\)
\(=x^2-2xy+xy-2y^2\)
\(=x\left(x-2y\right)+y\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+y\right)\)
g: Ta có: \(x^4-13x^2y^2+4y^4\)
\(=x^4-4x^2y^2+4y^4-9x^2y^2\)
\(=\left(x^2-2y^2\right)^2-\left(3xy\right)^2\)
\(=\left(x^2-3xy-2y^2\right)\left(x^2-3xy+2y^2\right)\)
\(=\left(x^2-3xy-2y^2\right)\left(x^2-xy-2xy+2y^2\right)\)
\(=\left[x\left(x-y\right)-2y\left(x-y\right)\right]\left(x^2-3xy-2y^2\right)\)
\(=\left(x-y\right)\left(x-2y\right)\left(x^2-3xy-2y^2\right)\)
h: Ta có: \(\left(x^2-2x\right)^2-2\left(x^2-2x\right)-3\)
\(=\left(x^2-2x\right)^2-3\left(x^2-2x\right)+\left(x^2-2x\right)-3\)
\(=\left(x^2-2x\right)\left(x^2-2x-3\right)+\left(x^2-2x-3\right)\)
\(=\left(x^2-2x-3\right)\left(x^2-2x+1\right)\)
\(=\left(x-3\right)\left(x+1\right)\cdot\left(x-1\right)^2\)
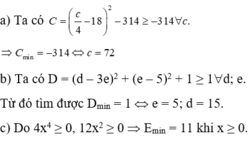
D= d2 + 10e2 - 6de - 10e + 26
= (d2 - 6de + 9e2) + (e2 - 10e + 25) + 1
= (d - 3e)2 + (e - 5)2 + 1 ≥ 1
Dấu "=" xảy ra khi d - 3e = e - 5 = 0 <=> \(\left\{{}\begin{matrix}e=5\\d=15\end{matrix}\right.\)
Vậy minD = 1 khi e=5; d=15
Cảm ơn bạn nhé!