Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hàm số \(y=\sin x\) giảm trên đoạn \(\left[\dfrac{\pi}{2};\dfrac{3\pi}{2}\right]\) và tăng trên đoạn \(\left[\dfrac{3\pi}{2};2\pi\right]\)
b) \(y=\sin x\) giảm trên \(\left[-\pi;-\dfrac{\pi}{2}\right]\), tăng trên \(\left[-\dfrac{\pi}{2};0\right]\)
c) \(y=\sin x\) tăng trên \(\left[-2\pi;-\dfrac{3\pi}{2}\right]\), giảm trên \(\left[-\dfrac{3\pi}{2};-\pi\right]\)

<=> cos ( x- pi/5) = cos pi/6
<=> x-pi/5 = pi/6 + 2k pi k thuộc z
x-pi/5 = -pi/6 + 2kpi
<=> x= 11pi/30 + 2kpi
x=pi/30 + 2k pi k thuộc z
sau đó bạn thay k vào ( k thuộc z)
nếu cái nào thỏa mãn thì lấy

a, Đồ thị hàm số \(y=cosx\): \(\left(A=\left(-\dfrac{\pi}{2};0\right);B=\left(\dfrac{\pi}{2};0\right)\right)\)
Dựa vào đồ thị ta có \(\left\{{}\begin{matrix}y_{min}=0\\y_{max}=1\end{matrix}\right.\)
b, Đồ thị hàm số \(y=sinx\): \(\left(A=\left(-\dfrac{\pi}{2};-1\right);A=\left(\dfrac{\pi}{2};1\right)\right)\)

Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
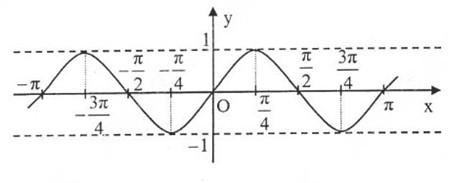
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)

3.3 d)
\(\sin8x-\cos6x=\sqrt{3}\left(\sin6x+\cos8x\right)\\ \Leftrightarrow\sin8x-\sqrt{3}\cos8x=\sqrt{3}\sin6x+\cos6x\\ \Leftrightarrow\sin\left(8x-\dfrac{\pi}{3}\right)=\sin\left(6x+\dfrac{\pi}{6}\right)\\ \Leftrightarrow\left[{}\begin{matrix}8x-\dfrac{\pi}{3}=6x+\dfrac{\pi}{6}+k2\pi\\8x-\dfrac{\pi}{3}=\pi-\left(6x+\dfrac{\pi}{6}\right)+k2\pi\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k\dfrac{\pi}{7}\end{matrix}\right.\)
3.4 a)
\(2sin\left(x+\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \Leftrightarrow2cos\left(\dfrac{\pi}{2}-x-\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \Leftrightarrow2cos\left(-x+\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \Leftrightarrow2cos\left(x-\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \)
Chia hai vế cho \(\sqrt{2^2+4^2}=2\sqrt{5}\)
Ta được:
\(\dfrac{1}{\sqrt{5}}cos\left(x-\dfrac{\pi}{4}\right)+\dfrac{2}{\sqrt{5}}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3}{4}\\ \)
Gọi \(\alpha\) là góc có \(cos\alpha=\dfrac{1}{\sqrt{5}}\)và \(sin\alpha=\dfrac{2}{\sqrt{5}}\)
Phương trình tương đương:
\(cos\left(x-\dfrac{\pi}{4}-\alpha\right)=\dfrac{3}{4}\\ \Leftrightarrow x=\pm arscos\left(\dfrac{3}{4}\right)+\dfrac{\pi}{4}+\alpha+k2\pi\)

a/ Trên đoạn xét thuộc cung thứ 4, sinx đồng biến
\(\Rightarrow y_{min}=sin\left(-\frac{\pi}{2}\right)=-1\) ; \(y_{max}=sin\left(-\frac{\pi}{3}\right)=-\frac{\sqrt{3}}{2}\)
b/ Trên đoạn xét thuộc cung phần tư thứ nhất và thứ 4, cosx luôn không âm
\(\Rightarrow y_{min}=cos\left(-\frac{\pi}{2}\right)=cos\left(\frac{\pi}{2}\right)=0\) ; \(y_{max}=cos0=1\)
c/ Trên đoạn xét thuộc cung phần tư thứ tư, sinx đồng biến
\(y_{min}=sin\left(-\frac{\pi}{2}\right)=-1\) ; \(y_{max}=sin0=0\)
d/ Trên đoạn xét thuộc cung phần tư thứ nhất (\(0< \frac{1}{4}< \frac{3}{2}< \frac{\pi}{2}\))
\(\Rightarrow cosx\) nghịch biến
\(y_{min}=y\left(\frac{3}{2}\right)=cos\left(\frac{3}{2}\right)\)
\(y_{max}=y\left(\frac{1}{4}\right)=cos\left(\frac{1}{4}\right)\)


