Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.A=5x-x^2\)
\(=-\left(x^2-5x\right)=-\left[\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\right]=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\)
\(\Rightarrow Max_A=\dfrac{25}{4}\) khi \(x=\dfrac{5}{2}\)
\(b.B=x-x^2=-\left(x^2-x\right)=-\left[\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\right]=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(\Rightarrow Max_B=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(c.C=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4-7\right)=-\left(x-2\right)^2+7\le7\)
\(\Rightarrow Max_C=7\Leftrightarrow x=2\)
a) Ta có:
\(A=5x-x^2\)
\(=-\left(x^2-5x\right)\)
\(=-\left(x^2-5x\right)-6,25+6,25\)
\(=-\left(x^2-5x+6,25\right)+6,25\)
\(=-\left(x-2,5\right)^2+6,25\)
Ta lại có:
\(\left(x-2,5\right)^2\ge0\)
\(\Rightarrow-\left(x-2,5\right)^2\le0\)
\(\Rightarrow-\left(x-2,5\right)^2+6,25\le6,25\)
\(\Rightarrow A\le6,25\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-2,5\right)^2=0\)
\(\Leftrightarrow x-2,5=0\)
\(\Leftrightarrow x=2,5\)
Vậy MaxA = 6,25 \(\Leftrightarrow x=2,5\)

bài 1 : a. x^3 +27 -54-x^3 =-27
b. 8x^3 +y^3 -8x^3 +y^3 =2y^3
c. (2x-1+2x+2)(2x-1-2x-2)=(4x+1).(-3)=-12x-3
d. a^3 +b^3 +3ab(a+b) -3ab(a+b)=a^3+b^3

a, ĐKXĐ: \(x\ne1;x\ne-1\)
b, Với \(x\ne1;x\ne-1\)
\(B=\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\left[\dfrac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\dfrac{5}{x^2-1}\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =4\)
=> ĐPCM

a) \(A=x^2+3x+4=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
\(minA=\dfrac{7}{4}\Leftrightarrow x=-\dfrac{3}{2}\)
b) \(B=2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(minB=\dfrac{7}{8}\Leftrightarrow x=\dfrac{1}{4}\)
c) \(C=5x^2+2x-3=5\left(x+\dfrac{1}{5}\right)^2-\dfrac{16}{5}\ge-\dfrac{16}{5}\)
\(minC=-\dfrac{16}{5}\Leftrightarrow x=-\dfrac{1}{5}\)
d) \(D=4x^2+4x-24=\left(2x+1\right)^2-25\ge-25\)
\(minD=-25\Leftrightarrow x=-\dfrac{1}{2}\)
e) \(E=x^2+6x-11=\left(x+3\right)^2-20\ge-20\)
\(minE=-20\Leftrightarrow x=-3\)
f) \(G=\dfrac{1}{4}x^2+x-\dfrac{1}{3}=\left(\dfrac{1}{2}x+1\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\)
\(minG=-\dfrac{4}{3}\Leftrightarrow x=-2\)
\(A=x^2+3x+4=\left(x^2+3x+\dfrac{9}{4}\right)+\dfrac{7}{4}=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\)
Do \(\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
\(minA=\dfrac{7}{4}\Leftrightarrow x+\dfrac{3}{2}=0\Leftrightarrow x=-\dfrac{3}{2}\)
Mấy câu còn lại làm tương tự nhé em^^

\(a,A=4-x^2+2x=4-\left(x^2-2x\right)=4-\left(x^2-2x+1-1\right)\)
\(=4-\left[\left(x-1\right)^2-1\right]=4-\left(x-1\right)^2+1=5-\left(x-1\right)^2\)
Vì \(\left(x-1\right)^2\ge0=>-\left(x-1\right)^2\le0=>5-\left(x-1\right)^2\le5\) (với mọi x)
Dấu "=" xảy ra \(< =>\left(x-1\right)^2=0< =>x=1\)
Vậy MaxA=5 khi x=1
\(b,B=4x-x^2=-x^2+4x=-\left(x^2-4x\right)=-\left(x^2-4x+4-4\right)\)
\(=-\left[\left(x-2\right)^2-4\right]=-\left(x-2\right)^2+4=4-\left(x-2\right)^2\)
Vì \(\left(x-2\right)^2\ge0=>-\left(x-2\right)^2\le0=>4-\left(x-2\right)^2\le4\) (với mọi x)
Dấu "=" xảy ra \(< =>\left(x-2\right)^2=0< =>x=2\)
Vậy MaxB=4 khi x=2
a) \(4-x^2+2x\)
\(=-\left(x^2-2x-4\right)\)
\(=-\left(x^2-2x+1-5\right)\)
\(=-\left(\left(x-1\right)^2-5\right)\)
\(=5-\left(x-1\right)^2\ge5\)
MIn A = 5 khi \(x-1=0=>x=1\)
b) \(4x-x^2\)
\(=-\left(x^2-4x+4-4\right)\)
\(=>-\left(\left(x-2\right)^2-4\right)\)
\(=4-\left(x-2\right)\ge4\)
MIN B = 4 khi \(x-2=0=>x=2\)
Ủng hộ nha tối rồi

a)a+b+c=9
=>(a+b+c)2=81
=>a2+b2+c2+2ab+2bc+2ca=81
Từ a2+b2+c2=141=>2ab+2bc+2ca=81-141=-60
=>2(ab+bc+ca)=-60=>ab+bc+ca=-30
b)x+y=1
=>(x+y)3=1
=>x3+3x2y+3xy2+y3=1
=>x3+y3+3xy(x+y)=1
=>x3+y3+3xy=1(Do x+y=1)
c)a3-3ab+2c=(x+y)3-3(x+y)(x2+y2)+2(x3+y3)
=x3+3x2y+3xy2+y3-3x3-3y3-3x2y-3xy2+2x3+2y3=0
d)đang tìm hướng giải

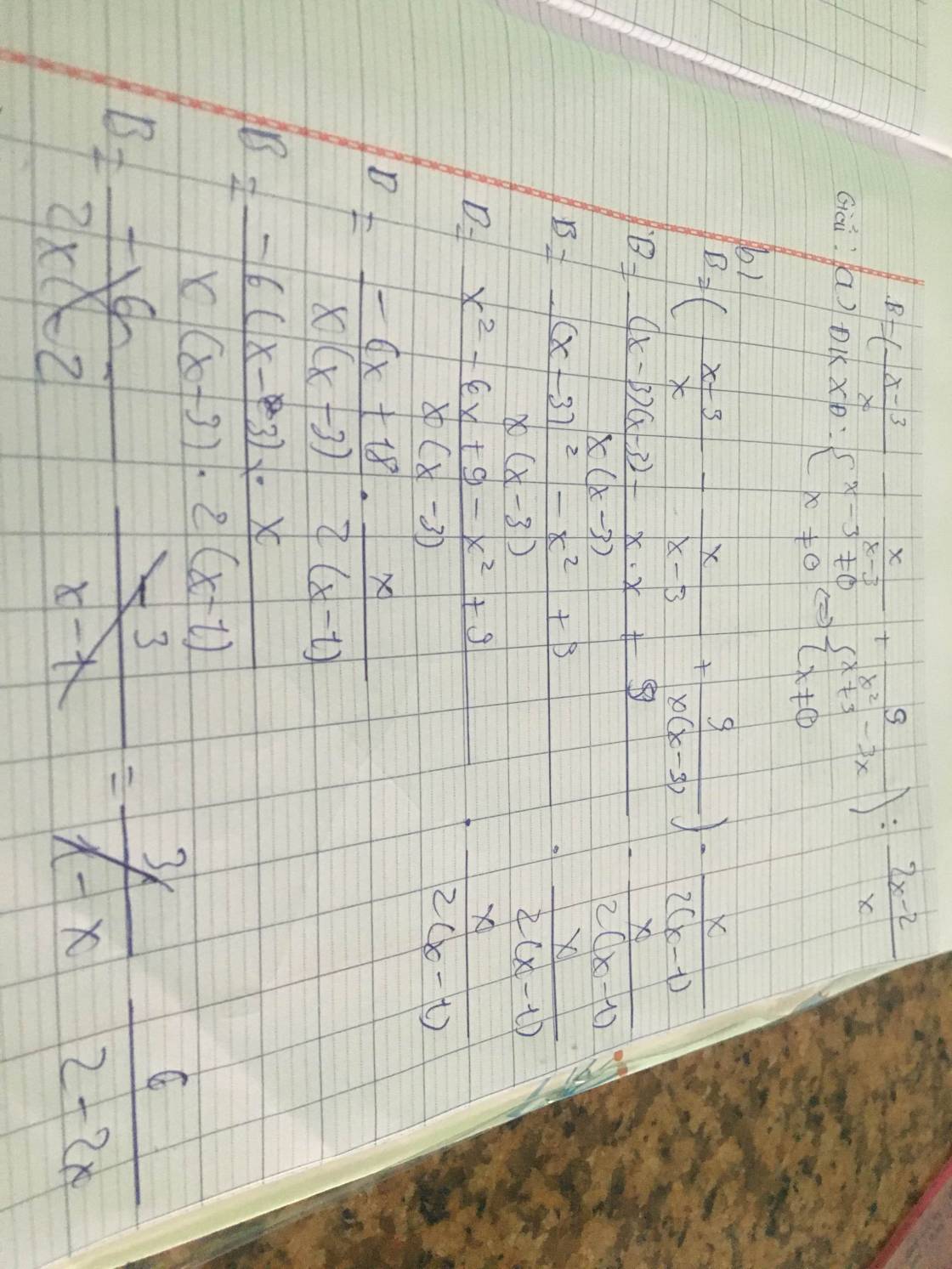 c/
c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.
\(A=x^2-4x+1\)
\(A=\left(x^2-4x+4\right)-3\)
\(A=\left(x-2\right)^2-3\)
Vì \(\left(x-2\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x-2\right)^2-3\ge-3\) với mọi x
\(\Rightarrow Amin=-3\Leftrightarrow x=2\)
\(B=4x^2+4x+11\)
\(B=\left(4x^2+4x+1\right)+10\)
\(B=\left(2x+1\right)^2+10\)
Vì \(\left(2x+1\right)^2\ge0\) với mọi x
\(\Rightarrow\left(2x+1\right)^2+10\ge10\) với mọi x
\(\Rightarrow Bmin=10\Leftrightarrow x=-\dfrac{1}{2}\)
\(C=\left(x-1\right)\left(x+3\right)\left(x+2\right)\left(x+6\right)\)
\(C=\left[\left(x-1\right)\left(x+6\right)\right]\left[\left(x+2\right)\left(x+3\right)\right]\)
\(C=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(C=\left(x^2+5x\right)^2-36\)
Vì \(\left(x^2+5x\right)^2\ge0\) với mọi x
\(\Rightarrow\left(x^2+5x\right)^2-36\ge-36\)
\(\Rightarrow Cmin=-36\Leftrightarrow x^2+5x=0\)
\(\Rightarrow x\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(D=5-8x-x^2\)
\(D=-\left(x^2+8x-5\right)\)
\(D=-\left(x^2+8x+16-16-5\right)\)
\(D=-\left(x^2+8x+16\right)+21\)
\(D=-\left(x+4\right)^2+21\)
Vì \(-\left(x+4\right)^2\le0\) với mọi x
\(\Rightarrow-\left(x+4\right)^2+21\le21\) với mọi x
\(\Rightarrow Dmax=21\Leftrightarrow x=-4\)
\(E=4x-x^2+1\)
\(E=-\left(x^2-4x-1\right)\)
\(E=-\left(x^2-4x+4-4-1\right)\)
\(E=-\left(x^2-4x+4\right)+5\)
\(E=-\left(x-2\right)^2+5\)
Vì \(-\left(x-2\right)^2\le0\) với mọi x
\(\Rightarrow-\left(x-2\right)^2+5\le5\) với mọi x
\(\Rightarrow Emax=5\Leftrightarrow x=2\)