
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left|x-\dfrac{2}{3}\right|-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)

3.a) Ta có: (x+1).(x-2) < 0
=> x+1 = 0 hoặc x-2 = 0
=> x = 0-1 = -1 hoặc x = 0+2 = 2
Vậy x = -1 hoặc x = 2
b) (x-2).(x+2/3) = ?
\(\Rightarrow\)x+1= 0 hoac x-2=0
\(\Rightarrow\)x+1=0 x-2=0
tu lam tiep

A = 5x² + 6
Do x² ≥ 0
⇒ 5x² ≥ 0
⇒ 5x² + 6 ≥ 6
Vậy giá trị nhỏ nhất của A là 6 khi x = 0
--------------------
B = 4(2x - 4)² + 2023
Do (2x - 4)² ≥ 0
⇒ 4(2x - 4)² ≥ 0
⇒ 4(2x - 4)² + 2023 ≥ 2023
Vậy giá trị nhỏ nhất của B là 2023 khi x = 2

\(A=\left(x-1\right)^2+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ 1>0.\\ \Rightarrow\left(x-1\right)^2+1\ge1\forall x\in R.\\ \Rightarrow A\ge1.\\ \Rightarrow A_{min}=1.\)
\(B=x^2+x^4-\dfrac{1}{2}.\\ x^2+x^4\ge0\forall x\in R.\\ \Leftrightarrow x^2+x^4-\dfrac{1}{2}\ge\dfrac{-1}{2}\forall x\in R.\\ \Rightarrow B\ge\dfrac{-1}{2}.\\ \Rightarrow B_{min}=\dfrac{-1}{2}.\)
\(D=\dfrac{2}{\left(x-1\right)^2}+1.\\ \left(x-1\right)^2\ge0\forall x\in R.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}\ge0.\\ \Leftrightarrow\dfrac{2}{\left(x-1\right)^2}+1\ge1\forall x\in R.\\ \Rightarrow D\ge1.\\ \Rightarrow D_{min}=1.\)

Bài 10:
a) Tìm Max
\(A=0,5-\left|x-3,5\right|\)
Có: \(\left|x-3,5\right|\ge0\)
\(\Rightarrow0,5-\left|x-3,5\right|\le0,5\)
Dấu = xảy ra khi: \(\left|x-3,5\right|=0\)
\(\Rightarrow x-3,5=0\Rightarrow x=3,5\)
Vậy: \(Max_A=0,5\) tại \(x=3,5\)
\(B=-\left|1,4-x\right|-2\)
Có: \(-\left|1,4-x\right|\le0\)
\(\Rightarrow-\left|1,4-x\right|-2\le-2\)
Dấu = xảy ra khi: \(-\left|1,4-x\right|=0\)
\(\Rightarrow1,4-x=0\Rightarrow x=1,4\)
Vậy: \(Max_B=-2\) tại \(x=1,4\)
b. Tìm Min
\(C=1,7+\left|3,4-x\right|\)
Có: \(\left|3,4-x\right|\ge0\)
\(\Rightarrow1,7+\left|3,4-x\right|\ge1,7\)
Dấu = xảy ra khi: \(\left|3,4-x\right|=0\)
\(\Rightarrow3,4-x=0\Rightarrow x=3,4\)
Vậy: \(Min_C=1,7\) tại \(x=3,4\)
\(D=\left|x+2,8\right|-3,5\)
Có: \(\left|x+2,8\right|\ge0\)
\(\Rightarrow\left|x+2,8\right|-3,5\ge-3,5\)
Dấu = xảy ra khi: \(\left|x+2,8\right|=0\)
\(\Rightarrow x+2,8=0\Rightarrow x=-2,8\)
Vậy: \(Min_D=-3,5\) tại \(x=-2,8\)

$A=(x-4)^2+1$
Ta thấy $(x-4)^2\geq 0$ với mọi $x$
$\Rightarroe A=(x-4)^2+1\geq 0+1=1$
Vậy GTNN của $A$ là $1$. Giá trị này đạt tại $x-4=0\Leftrightarrow x=4$
-------------------
$B=|3x-2|-5$
Vì $|3x-2|\geq 0$ với mọi $x$
$\Rightarrow B=|3x-2|-5\geq 0-5=-5$
Vậy $B_{\min}=-5$. Giá trị này đạt tại $3x-2=0\Leftrightarrow x=\frac{2}{3}$
$C=5-(2x-1)^4$
Vì $(2x-1)^4\geq 0$ với mọi $x$
$\Rightarrow C=5-(2x-1)^4\leq 5-0=5$
Vậy $C_{\max}=5$. Giá trị này đạt tại $2x-1=0\Leftrightarrow x=\frac{1}{2}$
----------------
$D=-3(x-3)^2-(y-1)^2-2021$
Vì $(x-3)^2\geq 0, (y-1)^2\geq 0$ với mọi $x,y$
$\Rightarrow D=-3(x-3)^2-(y-1)^2-2021\leq -3.0-0-2021=-2021$
Vậy $D_{\max}=-2021$. Giá trị này đạt tại $x-3=y-1=0$
$\Leftrightarrow x=3; y=1$
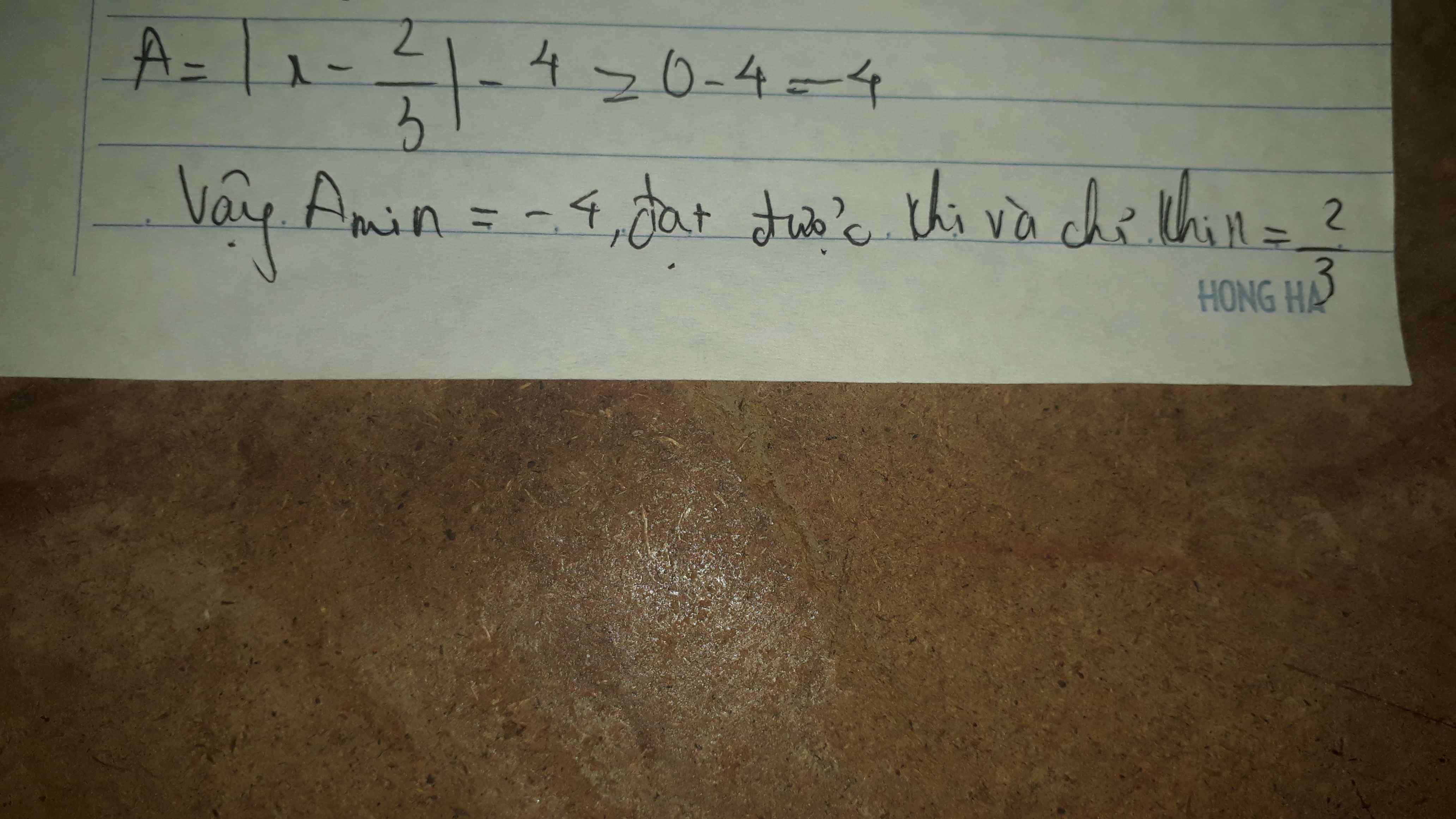
a) \(A=\left|x\right|+\frac{6}{13}\ge\frac{6}{13}\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x=0\)
b) \(B=\left|x+2,8\right|-7,9\ge-7,9\forall x\)
Dấu "=" xảy ra \(\Leftrightarrow x=-2,8\)
c) \(C=4\left|x-2\right|+\left(y-1\right)^2+2\ge2\forall x;y\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x=2\\y=1\end{cases}}\)
A = \(\left|x\right|+\frac{6}{13}\)
Vì \(\left|x\right|\ge0\forall x\)
\(\Rightarrow\left|x\right|+\frac{6}{13}\ge\frac{6}{13}\)
Dấu " = " xảy ra khi :
| x | = 0
=> x = 0