Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=2x^2+10x-1\)
=> \(B=2\left(x^2+5x\right)-1\)
=> \(B=2\left(x^2+2.x\frac{5}{2}+\frac{25}{4}\right)-\frac{27}{2}\)
=> \(B=2\left(x+\frac{5}{2}\right)^2-\frac{27}{2}\)
Có \(2\left(x+\frac{5}{2}\right)^2\ge0\)với mọi x
=> \(2\left(x+\frac{5}{2}\right)^2-\frac{27}{2}\ge\frac{-27}{2}\)
Dấu "=" xảy ra <=> \(\left(x+\frac{5}{2}\right)^2=0\)<=> \(x+\frac{5}{2}=0\)<=> \(x=\frac{-5}{2}\)
KL: Bmin = \(\frac{-27}{2}\)<=> \(x=\frac{-5}{2}\)
\(C=5x-x^2\)
=> \(C=-\left(x^2-5x\right)\)
=> \(C=-\left(x^2-2.x.\frac{5}{2}+\frac{25}{4}\right)+\frac{25}{4}\)
=> \(C=-\left(x-\frac{5}{2}\right)^2+\frac{25}{4}\)
Có \(\left(x-\frac{5}{2}\right)^2\ge0\)với mọi x
=> \(-\left(x-\frac{5}{2}\right)^2\le0\)
=> \(C=-\left(x-\frac{5}{2}\right)^2+\frac{25}{4}\le\frac{25}{4}\)
Dấu "=" xảy ra <=> \(\left(x-\frac{5}{2}\right)^2=0\)<=> \(x-\frac{5}{2}=0\)<=> \(x=\frac{5}{2}\)
KL: Cmax = \(\frac{25}{4}\)<=> \(x=\frac{5}{2}\)
B=2x2+10x-1=2(x2+5x-1/2)=2(x2+2*5/2*x+25/4-27/4)=2[x2+2*5/2*x+(5/2)2]-27/2=2(x+5/2)2-27/2
Ta có: (x+5/2)^2>=0(với mọi x)
=> 2(x+5/2)^2>=0(với mọi x)
=> 2(x+5/2)^2-27/2>=-27/2(với mọi x)
hay B>=-27/2( với mọi x)
Do đó, GTNN của B là -27/2 khi:
x+5/2=0
x=-5/2
Vậy GTNN của B là -27/2 khi x=-5/2
C=5x-x^2=-x^2+5x=-x^2+2*5/2*x-25/4+25/4=-[x^2-2*5/2*x+(5/2)^2]+25/4=-(x-5/2)^2+25/4
Ta có: (x-5/2)^2>=0(với mọi x)
=>-(x-5/2)^2<=0(với mọi x)
=> -(x-5/2)^2+25/4<=25/4(với mọi x) hay C<=25/4(với mọi x)
Do đó, GTLN của C là 25/4 khi: x-5/2=0
x=5/2
Vậy GTLN của C là 25/4 tại x=5/2

A = x2 - 6x + 11
Nhập phương trình vào máy tính lặp 3 lần dấu =
GTNN của A = 3
B = 2x2 + 10x - 1
Nhập phương trình vào máy tính lặp 3 lần dấu =
GTNN của B = \(-\frac{5}{2}\)
C = 5x - x2
=> C = -x2 + 5x
Nhập phương trình vào máy tính lặp 3 lần dấu =
GTLN của C = \(\frac{5}{2}\)

Bài 1:
a: \(A=x^2+2x+4\)
\(=x^2+2x+1+3\)
\(=\left(x+1\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x+1=0
=>x=-1
Vậy: \(A_{min}=3\) khi x=-1
b: \(B=x^2-20x+101\)
\(=x^2-20x+100+1\)
\(=\left(x-10\right)^2+1>=1\forall x\)
Dấu '=' xảy ra khi x-10=0
=>x=10
Vậy: \(B_{min}=1\) khi x=10
c: \(C=x^2-2x+y^2+4y+8\)
\(=x^2-2x+1+y^2+4y+4+3\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x-1=0 và y+2=0
=>x=1 và y=-2
Vậy: \(C_{min}=3\) khi (x,y)=(1;-2)
Bài 2:
a: \(A=5-8x-x^2\)
\(=-\left(x^2+8x\right)+5\)
\(=-\left(x^2+8x+16-16\right)+5\)
\(=-\left(x+4\right)^2+16+5=-\left(x+4\right)^2+21< =21\forall x\)
Dấu '=' xảy ra khi x+4=0
=>x=-4
b: \(B=x-x^2\)
\(=-\left(x^2-x\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
c: \(C=4x-x^2+3\)
\(=-x^2+4x-4+7\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7< =7\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
d: \(D=-x^2+6x-11\)
\(=-\left(x^2-6x+11\right)\)
\(=-\left(x^2-6x+9+2\right)\)
\(=-\left(x-3\right)^2-2< =-2\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3

A+1 = x^2+6x+9/x^2+1 = (x+3)^2/x^2+1 >= 0
=> A >= -1
Dấu "=" xảy ra <=> x+3=0 <=> x=-3
Vậy GTNN của A = -1 <=> x=-3
Tk mk nha

1:
=x^2-6x+9-4=(x-3)^2-4>=-4
Dấu = xảy ra khi x=3
3: =-y^2-4y-4+13
=-(y+2)^2+13<=13
Dấu = xảy ra khi y=-2
4: D=x^2-8>=-8
Dấu = xảy ra khi x=0



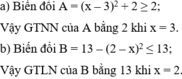
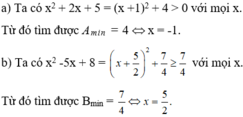
\(a.A=x^2+5x+7\\ =\left[x^2+2\cdot x\cdot\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2\right]+\dfrac{3}{4}\\ =\left(x+\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra: `x+5/2=0<=>x=-5/2`
\(b.B=6x-x^2-5\\ =-\left(x^2-6x+9\right)+4\\ =-\left(x-3\right)^2+4\le4\forall x\)
Dấu "=" xảy ra: `x-3=0<=>x=3`