Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Để ý thấy lời giải bài toán sai ở bước 3 do m có thể nhỏ hơn 0

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

Đáp án A
Hoành độ giao điểm là nghiệm của PT:
x − 4 = − 2 x + 5 x − 2 ⇔ x 2 − 6 x + 8 = − 2 x + 5 x ≠ 2
⇔ x 2 − 4 x − 13 = 0 . Vậy trung điểm I của MN có hoành độ x = 2 ⇒ y = − 2 .

Chọn B.
Phương pháp:
Giải phương trình hoành độ giao điểm của hai đồ thị hàm số. Tìm tọa độ giao điểm M và N. Tìm tọa độ trung điểm I của MN.
Cách giải:
Phương trình hoành độ giao điểm của đồ thị hai hàm số
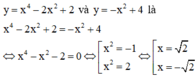

Xét hàm số y = f x = x - 2 + 4 - x trên đoạn 2 , 4 có:

Ta có:
![]()
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = x - 2 + 4 - x lần lượt là M = 2 ; m = 2
Chọn: D

ta tính
\(y'=3x^2-6x=3x\left(x-2\right)\)
giải pt y'= 0 ta có \(3x\left(x-2\right)=0\) suy ra x=0 hoặc x=2
x y' -3 0 1 2 0 0 y + -55 -1 -3 - -
nhìn vào bảng bt ta có giái trị lớn nhất của hàm số =3 khi x=0, hàm số đạt giá trị nhỏ nhất =-55 khi x=-3
hàm số đạt giái trị lớn nhất =-1 khi x=0, nhỏ nhất =-55 khi x=-3

Chọn C.
Tập xác định của hàm số ![]()
Cách 1: Bấm máy tính. Với máy 580vn chọn start:-2, end: 2, step: 2/9 có: ![]()
thử thấy phương án C gần nhất với kết quả này nên ta chọn C.
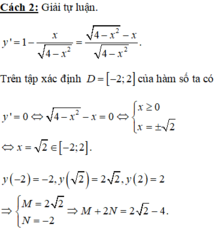

ta có
\(\)\(y=\frac{1}{3}\log^3_{\frac{1}{2}}x+\log^2_{\frac{1}{2}}x-3\log_{\frac{1}{2}}x+1\)
Đặt =\(t=\log_{\frac{1}{2}}x\) ta có
\(y=\frac{1}{3}t^3+t^2-3t+1\)
với \(\frac{1}{4}\le x\le4\Leftrightarrow\frac{1}{4}\le\left(\frac{1}{2}\right)^t\le4\Leftrightarrow-2\le t\le2\)
thay vì tính GTLN,GTNN của hàm số y trên [1/4;4] ta tính GTLN,GTNN của hàm số trên [-2;2]
ta tính \(y'=t^2+2t-3\)
ta tính y'=0 suy ra t=1(loại);t=-3(loại)
ta tính y(2)=\(\frac{5}{3}\);y(-2)=\(\frac{-25}{3}\)
vậy GTNN của y=\(\frac{-25}{3}khi\log_{\frac{1}{2}}x=-2\Rightarrow x=4\)
hàm số đạt GTLN y=\(\frac{5}{3}\) khi \(\log_{\frac{1}{2}}x=2\Leftrightarrow x=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
Chọn D