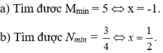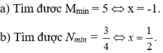
a) M = 2...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. \(1,a,A=x^2-6x+25\) \(=x^2-2.x.3+9-9+25\) \(=\left(x-3\right)^2+16\) Ta có : \(\left(x-3\right)^2\ge0\)Với mọi x \(\Rightarrow\left(x-3\right)^2+16\ge16\) Hay \(A\ge16\) \(\Rightarrow A_{min}=16\) \(\Leftrightarrow x=3\) b) \(M=\frac{x^2+1}{x-1}=\frac{x^2-1}{x-1}+\frac{2}{x-1}=\frac{\left(x-1\right)\left(x+1\right)}{x-1}+\frac{2}{x-1}=x+1+\frac{2}{x-1}\) Áp dụng bđt Cô si cho 2 số dương ta được: \(x-1+\frac{2}{x-1}\ge2\sqrt{\left(x-1\right).\frac{2}{x-1}}=2\sqrt{2}\) =>\(M=x+1+\frac{2}{x-1}\ge2\sqrt{2}+2\) Dấu "=" xảy ra khi \(x=\sqrt{2}+1\) c) \(N=\left(x-1\right)\left(x+5\right)\left(x^2+4x+5\right)=\left(x^2+4x-5\right)\left(x^2+4x+5\right)=\left(x^2+4x\right)^2-25\) \(\left(x^2+4x\right)^2\ge0\Rightarrow\left(x^2+4x\right)^2-25\ge-25\) Dấu "=" xảy ra khi (x2+4x)2=0 <=> x2+4x=0 <=> x(x+4)=0 <=> x=0 hoặc x=-4 A=(x−1)2+8≥8Amin=8⇔x=1B=(x+3)2−12≥−12Bmin=−12⇔x=−3C=x2−4x+3+9=(x−2)2+8≥8Cmin=8⇔x=2E=−(x+2)2+11≤11Emax=11⇔x=−2F=9−4x2≤9Fmax=9⇔x=0 HT A=x2-2x+9 Ta có: A=x^2-2x+9 => A=(x^2-2x+1)+8 =>A=(x-1)^2+8 vì (x-1)^2 > 0 với mọi x => (x-1)^2+8> 8 với mọi x Dấu "=" xáy ra khi: (x-1)^2=0=>x-1=0=>x=0+1=>x=1 Vậy Amin = 8 khi x=1 B=x^2+6x-3 =>B=-(x^2-6x+3) =>B=-(x^2-2.3x+3^2)-3 =>B=-(x-3)^2-3 vì -(x-3)^2 < 0 với mọi x =>-(x-3)^2-3< -3 với mọi x Dấu '=' xảy ra khi x-3=0=>x=0+3=>x=3 Vậy B(min)=-3 khi x=3 chỗ này hình như là Bmax xem lại đề nhé D=-x^2-4x+7 =>D=-x^2-2.2x+4+3 =>D=(-x^2-2.2x+4)+3 =>D=(-x-2)^2+3 Vì (-x-2)^2 <0 với mọi x =>(-x-2)^2+3<3 với mọi x Dấu "=" xảy ra khi x-2=0=>x=0+2=>x=2 Vậy Dmax=3 khi x=2 E=5-4x^2+4x =>E=-4x^2+4x+5 =>E=(-2x)^2+2.2x+4+1 =>E=[(-2x)^2+2.2x+4] =>E=(-2x+2)^2+1 Vì: (-2x+2)^2 < 0 với mọi x =>(-2x+2)^2+1 < 1 với mọi x Dấu "=" xảy ra khi 2x+2=0=>2x=-2=>x=-1 Vậy Emax=1 khi x=-1 a_ \(B=\left(x-3\right)^2+\left(x-1\right)^2\ge0\) \(MinB=0\Rightarrow\hept{\begin{cases}x-3=0\\x-1=0\end{cases}}\Rightarrow\hept{\begin{cases}x=3\\x=1\end{cases}}\) b) \(C=x^2+4xy+5y^2-2y\) \(=\left(x+2y\right)^2+y^2-2y\) \(=\left(x+2y\right)^2+y^2-2y\ge-2y\) \(MinC=-2y\Leftrightarrow\hept{\begin{cases}x+2y=0\\y=0\end{cases}\Rightarrow x=y=0}\)
K
Khách
CM
Cao Minh Tâm
4 tháng 7 2017
Đúng(1)
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2
22 tháng 10 2021
TM
14 tháng 7 2017
KA
8 tháng 11 2021
8 tháng 11 2021
12 tháng 8 2016
