Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Đặt z = a + b i , a , b ∈ ℝ . Ta có 1 − i z 2 + 2 + 2 i z 2 + 2 z z + i = 0 .
Với a 2 + b 2 > 0 ⇒ z ≠ 0 ; z 2 = z . z ¯ . Ta có
1 ⇔ 1 − i . z . z ¯ + 2 + 2 i z 2 + 2 z z + i = 0 ⇔ 1 − i z ¯ + 2 + 2 i z + 2 z + i = 0
⇔ 1 − i a − b i + 2 + 2 i a + b i + 2 a + b + 1 i = 0
⇔ a − b − a + b i + 2 a − 2 b + 2 a + 2 b i + 2 a + 2 b + 2 i = 0
⇔ 5 a − 3 b + a + 3 b + i = 0 ⇔ 5 a − 3 b = 0 a + 3 b = − 2 ⇔ a = − 1 3 b = − 5 9 ⇒ F = 3 5

Đáp án C
Phương pháp : Xác định hàm số f’(x) từ đó tính được ![]()
Cách giải : Ta dễ dàng tìm được phương trình parabol là
![]()
![]()
Đồ thị hàm số đi qua gốc tọa độ ![]()
![]()
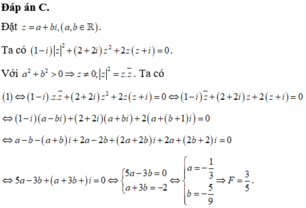

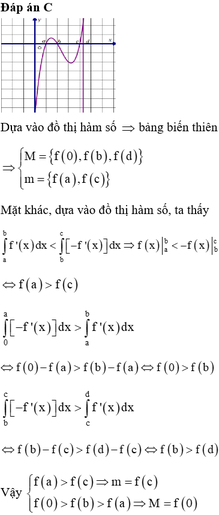

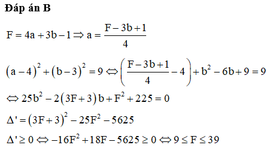

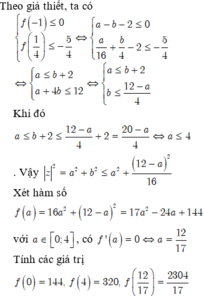
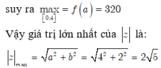
Đáp án C
Phương pháp: Thêm bớt hạng tử để được các hằng đẳng thức.
Sử dụng kết quả A 2 + B 2 + C ≥ C để tìm min F và chú ý tìm điều kiện để dấu “=” xảy ra. 2
Cách giải: F = a 4 b 4 + b 4 a 4 − a 2 b 2 + b 2 a 2 + a b + b a
= a 2 b 2 − 1 2 + b 2 a 2 − 1 2 + a b + b a 2 + a b + b a − 4 ≥ a 2 + b 2 a b − 4 ≥ 2 − 4 = − 2
Dấu “=” xảy ra ⇔ a ; b = − 1 ; 1 hoặc a ; b = 1 ; − 1
Vậy M i n y = − 2 tại a ; b = − 1 ; 1 hoặc a ; b = 1 ; − 1