
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tìm k để 3 điểm sau thẳng hàng M ( 2; -1), N (1; 1 ) và P ( 3; k + 1).
Gọi phương trình đường thẳng đi qua 2 điểm M, N là y = ax + b
Khi đó ta có:
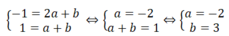
Phương trình đường thẳng MN là: y = - 2x + 3
Để 3 điểm M, N, P thẳng hàng thì P nằm trên đường thẳng MN
⇔ k + 1 = -2.3 + 3 ⇔ k + 1 = -3 ⇔ k = -4 (Thỏa mãn ĐK)


a) (d) đi qua điểm (1;2)
<=> 2 = k + 1 + k
<=> 1 = 2k
<=> k = 0,5
Vậy k = 0,5 thì (d) đi qua (1;2)
b) Để (d) // đgth y = 2x + 3
\(\Leftrightarrow\hept{\begin{cases}k+1=2\\k\ne3\end{cases}\Leftrightarrow\hept{\begin{cases}k=1\\k\ne3\end{cases}\Rightarrow}k=1}\)
Vậy k =1 thì (d) // đgth y = 2x +3
c) Gọi điểm cố định là (d) đi qua là (x0;y0)
Ta có y0 = ( k +1) x0 + k
<=> y0 = kx0 + x0+k
<=> y0 - x0 - k ( x0 + 1) = 0 \(\forall\)k
Để pt nghiệm đúng với mọi k <=> \(\hept{\begin{cases}x_0+1=0\\y_0-x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=-1\end{cases}}}\)
Điểm cố định (d) luôn đi qua là ( -1;-1)

Lời giải:
$K(-2;1)\in (d)$ khi mà:
$y_K=(m-2)x_K+m+3$
$\Leftrightarrow 1=(m-2)(-2)+m+3$
$\Leftrightarrow 1=-2m+4+m+3=-m+7$
$\Leftrightarrow m=6$

với x=-3 ta có tung độ tương ứng của đường thẳng thứ nhất là :
\(y_1=\left(5k+2\right).\left(-3\right)-3=-15k-9\)
tương tự ta có \(y_2=\left(3k-2\right).\left(-3\right)+2=-9k+8\)
để hai đường thẳng cắt nhau tại điểm có hoành độ bằng -3 thì
\(y_1=y_2\Leftrightarrow-15k-9=-9k+8\Leftrightarrow k=-\frac{17}{6}\)