DV
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 3 2023
\(\dfrac{4^5\cdot9^4-2\cdot6^9}{2^{10}\cdot3^8+6^8\cdot20}=\dfrac{2^{10}\cdot3^8-2\cdot2^9\cdot3^8\cdot3}{2^{10}\cdot3^8+2^8\cdot3^8\cdot2^2\cdot5}=\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^{10}\cdot3^8\cdot5}\)
\(=\dfrac{2^{10}\cdot3^8\left(1+3\right)}{2^{10}\cdot3^8\left(1+5\right)}=\dfrac{4}{6}=\dfrac{2}{3}\)
PT
1
3 tháng 10 2021
Bài 1:
a: \(x^2+5x=x\left(x+5\right)\)
Để biểu thức này âm thì \(x\left(x+5\right)< 0\)
hay -5<x<0
b: \(3\left(2x+3\right)\left(3x-5\right)< 0\)
\(\Leftrightarrow-\dfrac{3}{2}< x< \dfrac{5}{3}\)
YN
21 tháng 6 2022
\(A=\left(x-4\right)^2+1\)
Ta có: \(\left(x-4\right)^2\ge0\Rightarrow\left(x-4\right)^2+1\ge1\Rightarrow A\ge1\)
\(A_{min}=1\Leftrightarrow x=4\)
\(B=\left|3x-2\right|-5\)
Ta có: \(\left|3x-2\right|\ge0\Rightarrow\left|3x-2\right|-5\ge-5\Rightarrow B\ge-5\)
\(B_{min}=-5\Leftrightarrow x=\dfrac{2}{3}\)
\(C=5-\left(2x-1\right)^4\)
Ta có: \(\left(2x-1\right)^4\ge0\forall x\Rightarrow-\left(2x-1\right)^4\le0\forall x\Rightarrow5-\left(2x-1\right)^4\le5\Rightarrow C\le5\)
\(C_{max}=5\Leftrightarrow x=\dfrac{1}{2}\)
\(D=-3\left(x-3\right)^2-\left(y-1\right)^2-2021\)
Ta có: \(\left\{{}\begin{matrix}-3\left(x-3\right)^2\le0\forall x\\-\left(y-1\right)^2\le0\forall y\end{matrix}\right.\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2\le0\forall x,y\Rightarrow-3\left(x-3\right)^2-\left(y-1\right)^2-2021\le-2021\Rightarrow D\le-2021\)
\(D_{max}=-2021\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
\(E=-\left|x^2-1\right|-\left(x-1\right)^2-y^2-2020\)
\(=-\left|\left(x-1\right)\left(x+1\right)\right|-\left(x-1\right)^2-y^2-2020\)
Ta có: \(\left\{{}\begin{matrix}\left|\left(x-1\right)\left(x+1\right)\right|\ge0\forall x\Rightarrow-\left|\left(x-1\right)\left(x+1\right)\right|\le0\\\left(x-1\right)^2\ge0\forall x\Rightarrow-\left(x-1\right)^2\le0\\y^2\ge0\Rightarrow-y^2\le0\end{matrix}\right.\Rightarrow E\le-2020\)
\(E_{max}=-2020\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
TM
21 tháng 6 2016
bài 1:
\(\left(\frac{1}{2}-2\right).\left(\frac{1}{3}-x\right)>0\)
\(\Leftrightarrow\left(-\frac{3}{2}\right)\left(\frac{1}{3}-x\right)>0\)
Để biểu thức \(\left(\frac{1}{2}-2\right)\left(\frac{1}{3}-x\right)\) nhận giá trị dương thì \(-\frac{3}{2}\)và \(\frac{1}{3}-x\)phải cùng âm
\(\Leftrightarrow\frac{1}{3}-x< 0\)
\(\Leftrightarrow x>\frac{1}{3}\)
Vậy \(x>\frac{1}{3}\)thì biểu thức\(\left(\frac{1}{2}-2\right)\left(\frac{1}{3}-x\right)\) nhận giá trị dương
bài 2:
a)Để \(\frac{x^2-2}{5x}\) nhận giá trị âm thì x2-2<0 hoặc 5x<0
+)Nếu x2-2<0
=>x2<2
=>x<\(\sqrt{2}\)
+)Nếu 5x<0
=>x<0
Vậy x<\(\sqrt{2}\)hoặc x<0 thì biểu thức \(\frac{x^2-2}{5x}\)nhận giá trị âm
b)Để E nhận giá trị âm thì \(\frac{x-2}{x-6}\)nhận giá trị âm
=>x-2<0 hoặc x-6<0
+)Nếu x-2<0
=>x<2
+)Nếu x-6<0
=>x<6
Vậy x<2 hoặc x<6 thì biểu thức E nhận giá trị âm
HT
1
30 tháng 10 2023
Để tìm các giá trị nguyên của x sao cho biểu thức C = 3/x + 1 mang giá trị nguyên, ta cần xem xem giá trị của x có thể nhận được những giá trị nào.
Với biểu thức C = 3/x + 1, ta thấy x không thể bằng 0 vì không thể chia cho 0.
Nếu x = 1, thì C = 3/1 + 1 = 4.
Nếu x = 2, thì C = 3/2 + 1 = 2.5 + 1 = 3.5.
Nếu x = 3, thì C = 3/3 + 1 = 1 + 1 = 2.
Nếu x = 4, thì C = 3/4 + 1 = 0.75 + 1 = 1.75.
Như vậy, ta thấy chỉ có x = 1 và x = 3 làm cho biểu thức C mang giá trị nguyên.
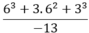
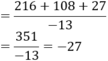
6^2.(6+3)+3^3/-13=36.3^2+3^3/-13=3^2(36+3)/-13=9.39/-13=-27
2^10.3^8-2.3^9.2^9 / 2^10.3^8+3^8.2^8.2^2.5
=2^10.3^8(1-3) / 2^10.3^8(1+5)
=-2/6=-1/3