
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có A : B

Để giá trị của đa thức A = 2 x 3 – 3 x 2 + 2x + 2 chia hết cho giá trị của đa thức B = x 2 + 1 thì
5 ⁝ ( x 2 + 1)
Hay ( x 2 + 1) Є U(5) = {-1; 1; -5; 5}
+) x 2 + 1 = -1 ó x 2 = -2 (VL)
+) x 2 + 1 = 1 ó x 2 = 0ó x = 0 (tm)
+) x 2 + 1 = -5 ó x 2 = -6 (VL)
+) x 2 + 1 = 5 ó x 2 = 4 ó x = ± 2 ™
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = -2; x = 2
Đáp án cần chọn là: A

\(2x^3-3x^2+x+a=\left(x+2\right)\left(2x^2-7x+15\right)+\left(a-30\right)=Q\left(x\right).\left(x+2\right)\)
=> x=-2 thì \(2.\left(-2\right)^2-3\left(-2\right)^2+\left(-2\right)+a=Q\left(x\right).0=0\)
<=> -16 -12 -2 +a =0
<=> a -30 =0
=> a= 30.

Thực hiện phép chia:
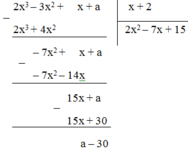
2x3 – 3x2 + x + a chia hết cho x + 2
⇔ số dư = a – 30 = 0
⇔ a = 30.
Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.
2x3 – 3x2 + x + a
= 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30
(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)
= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30
= (2x2 – 7x + 15)(x + 2) + a – 30
2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.

a: \(\dfrac{A}{B}=\dfrac{x^3+x^2+2x^2+2x+x+1-3}{x+1}=x^2+2x+1-\dfrac{3}{x+1}\)
b: Để A chia hết cho B thì \(x+1\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{0;-2;2;-4\right\}\)

Đa thức \(f\left(x\right)=2x^3-3x^2+x+a\) chia hết cho đa thức \(x+2\)
\(\Leftrightarrow\)\(f\left(-2\right)=0\)
\(\Leftrightarrow\)\(2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a=0\)
\(\Leftrightarrow\)\(-30+a=0\)
\(\Leftrightarrow\)\(a=30\)
Vậy \(a=30\)thì \(2x^3-3x^2+x+a\)chia hết cho \(x+2\)
p/s: bn có thế lm theo cách truyền thống: đặt tính chia ra rồi đặt dư = 0 và tìm a
hoặc dùng hệ số bất định
2x^3-3x^2+x+a | x+2
------------------|-------------
2x^3-3x^2 | 2x^2-7x+15
2x^2+4x^2
-7x^2+x
-7x^2-14x
15x+a
15x+30
\(2x^3-3x^2+x+a\div x+2\)
Để đa thức \(2x^3+3x^2+x+a⋮x+2\)
\(\Rightarrow15x+a=15x+30\)
\(\Rightarrow a-30=0\Rightarrow a=30\)

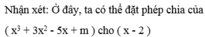
để tìm số dư, rồi cho số dư đó bằng 0, từ đó tìm được giá trị của m.
Mở rộng: Bài toán này ta áp dụng phân tích đa thức thành nhân tử để giải toán


a: Khi x=-1 thì B=2*(-1)^2+1+1=4
b: Để A chia hết cho B thì
\(2x^3-x^2+x+6x^2-3x+3+a-3⋮2x^2-x+1\)
=>a-3=0
=>a=3
c: Để B=1 thì 2x^2-x=0
=>x=0 hoặc x=1/2

a: \(\Leftrightarrow2x^4-2x^3+2x^2+3x^3-3x^2+3x-2x^2+2x+2+a-2⋮x^2-x+1\)
=>a=2

Đặt \(f\left(x\right)=2x^3-3x^2+x+a\)
Ta có: phép chia \(f\left(x\right)\) cho \(x+2\) có dư là \(R=f\left(-2\right)\)
\(\Rightarrow f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a\)
\(f\left(-2\right)=2.\left(-8\right)-3.4-2+a\)
\(f\left(-2\right)=-16-12-2+a\)
\(f\left(-2\right)=-20+a\)
Để \(f\left(x\right)\) chia hết cho \(x+2\) thì \(R=0\) hay \(f\left(-2\right)=0\)
\(\Rightarrow-20+a=0\Leftrightarrow a=20\)