
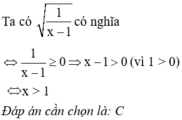
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

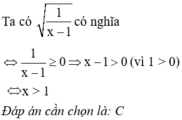

a) ĐKXĐ: \(x+5\ge0\Leftrightarrow x\ge-5\)
b) ĐKXĐ: \(7-x\ge0\Leftrightarrow x\le7\)
c) ĐKXĐ: \(x+3>0\Leftrightarrow x>-3\)
d) ĐKXĐ: \(x-3< 0\Leftrightarrow x< 3\)

a)
\(\sqrt{2x+10}+\frac{1}{x^2+4}\)
Căn thức có nghĩa khi
\(\begin{cases}2x+10\ge0\\x^2-4\ne0\end{cases}\)
\(\Leftrightarrow\begin{cases}x\ge-5\\\begin{cases}x\ne2\\x\ne-2\end{cases}\end{cases}\)
Vật căn thức có nghĩa khi \(x>-6;x\ne\pm2\)
b)
\(\sqrt{\frac{x^2+1}{x-1}}\)
Căn thưc có nghĩa khi
\(\begin{cases}\left(x^2+1\right)\left(x-1\right)\ge0\\x-1\ne0\end{cases}\)
Mà \(x^2+1\ge1\) => x - 1 >0
\(x+1>0\)
\(\Leftrightarrow x>-1\)

a: ĐKXĐ: 5-4x>=0
=>x<=5/4
b: ĐKXĐ: x thuộc R
c: ĐKXĐ: x-2<0
=>x<2

a: ĐKXĐ: x>=0; x<>1
\(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}=\dfrac{x+\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
b: Khi x=9/4 thì A=3/2:1/2=3/2*2=3

a: ĐKXĐ: x>=0; x<>1
b \(A=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
c: Khi x=9-4 căn 5 thì \(A=\dfrac{1}{\sqrt{5}-2+2}=\dfrac{\sqrt{5}}{5}\)
d: căn x+2>=2
=>A<=1/2
Dấu = xảy ra khi x=0


a,Để \(\sqrt{x^2-8x-9}\) có nghĩ thì
\(x^2-8x-9\ge0\)
\(\Leftrightarrow x^2+x-9x-9\ge0\)
\(\Leftrightarrow x\left(x+1\right)-9\left(x+1\right)\ge0\)
\(\Leftrightarrow\left(x+1\right)\left(x-9\right)\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1\ge0\\x-9\ge0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x\ge-1\\x\ge9\end{cases}\Rightarrow}x\ge9\)
\(or\orbr{\begin{cases}x+1\le0\\x-9\le0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x\le-1\\x\le9\end{cases}\Rightarrow}x\le-1\)
\(Để\sqrt{4-9x^2}\text{có nghĩa}\)
\(\Rightarrow4-9x^2\ge0\)
\(\Leftrightarrow\left(2-3x\right)\left(2+3x\right)\ge0\)
\(\Leftrightarrow-\frac{2}{3}\le x\le\frac{2}{3}\)