Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
y ' = x 2 - 2 x + ( m - 1 ) .
Hàm số đồng biến trên R ⇔ y' ≥ 0 ∀x ∈ R
⇒ Δ = ( - 1 ) 2 - ( m - 1 ) = - m + 2 ≤ 0 ⇔ m > 2

y'=1/3*3x^2(m-1)-(m-1)2x+1
=x^2(m-1)-x(2m-2)+1
Để hàm số đồng biến trên R thì y'>0 với mọi x
=>m-1<>0 và (2m-2)^2-4(m-1)>0
=>m<>1 và 4m^2-8m+4-4m+4>0
=>4m^2-12m+8>0 và m<>1
=>m^2-3m+2>0 và m<>1
=>m>2 hoặc m<1

\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

\(y'=mx^2-2\left(m-1\right)x+3\left(m-2\right)\)
\(y'\ge0\) ; \(\forall x\ge2\)
\(\Leftrightarrow mx^2-2\left(m-1\right)x+3\left(m-2\right)\ge0\) ; \(\forall x\ge2\)
\(\Leftrightarrow mx^2-2mx+3m\ge6-x\)
\(\Leftrightarrow m\left(x^2-2x+3\right)\ge6-x\)
\(\Leftrightarrow m\ge\dfrac{6-x}{x^2-2x+3}\)
\(\Rightarrow m\ge\max\limits_{x\ge2}\dfrac{6-x}{x^2-2x+3}=\dfrac{4}{3}\)
Vậy \(m\ge\dfrac{4}{3}\)
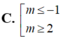
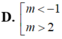
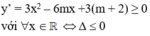

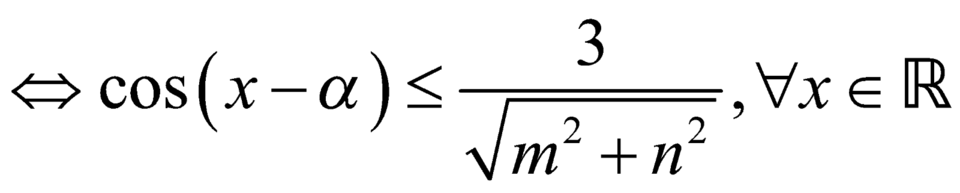
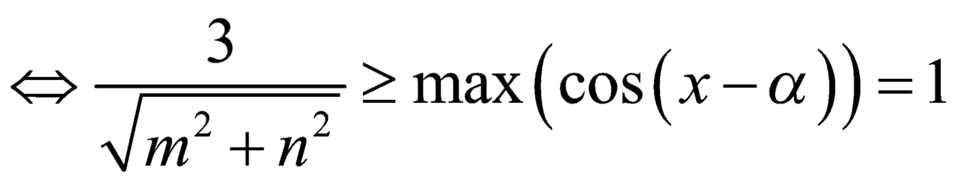

Chọn D