Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ABCD là hình vuông
\(\Rightarrow\Delta ABD\&\Delta ACD\) là tam vuông cân
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|.\sqrt[]{2}\\\left|\overrightarrow{BD}\right|=\left|\overrightarrow{AB}\right|.\sqrt[]{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|\overrightarrow{AC}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\\\left|\overrightarrow{BD}\right|=\dfrac{\sqrt[]{2}}{2}.\sqrt[]{2}=1\end{matrix}\right.\)
\(\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.\left|\overrightarrow{AC}\right|\) (O là trung điểm AC)
\(\Rightarrow\left|\overrightarrow{OA}\right|=\left|\overrightarrow{AO}\right|=\dfrac{1}{2}.1=\dfrac{1}{2}\)

Gọi số điểm 4 bài đầu là a, điểm bài cuối là b
\(\Rightarrow\hept{\begin{cases}a,b\inℕ\\a,b\le100\\\frac{4a+b}{5}=82\end{cases}\Leftrightarrow4a+b=410}\)
Lại có \(\hept{\begin{cases}a\le100\Rightarrow b\ge10\\410\equiv2\left(mod4\right),4a⋮4\end{cases}\Rightarrow\hept{\begin{cases}10\le b\le100\\b\equiv2\left(mod4\right)\end{cases}}}\)
\(\Rightarrow b\in\left\{10;14;18;...;94;98\right\}\)
Số điểm kiểm tra cuối của Laila có thể nhận số giá trị là:
\(\left(98-10\right):4+1=23\left(gt\right)\)
vậy ...
Có 5 đáp án cho sẵn của bài là:
(A)4 (B)5 (C)9 (D)10 (E)18
Đè thi thử AMC 8 2018

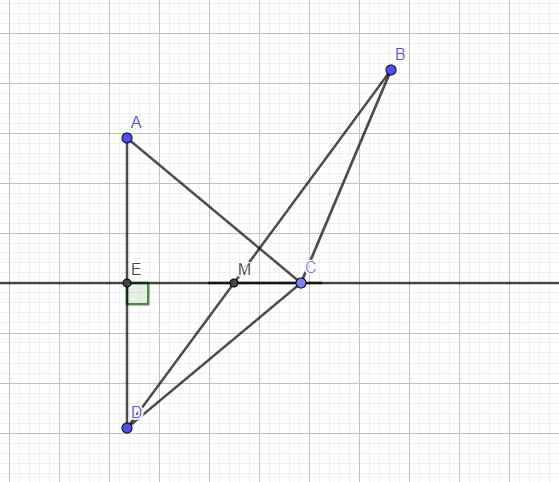
Gọi D là điểm đối xứng A qua d \(\Rightarrow\) d là trung trực AD \(\Rightarrow CA=CD\)
Nối BD cắt d tại M
Do BD là đường thẳng và BCD là đường gấp khúc nên ta luôn có:
\(BC+CD\ge BM+MD\)
\(\Leftrightarrow CB+CA\ge BD\)
Dấu "=" xảy ra khi và chỉ khi C trùng M
\(\Rightarrow\) Độ dài CA+CB ngắn nhất khi C là giao điểm của BD và d, trong đó D là điểm đối xứng với A qua d




Ví dụ 1 là gì bạn?