Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì f(x) chia cho x2-5x+6 được thương là 1-x2 và còn dư nên f(x) có bậc 4 và đa thức dư bậc cao nhất là 1.
Gọi f(x)=(x-2)(x-3)(1-x2)+ax+b
Ta có f(2)=2 vaf(3)=7 thay vào tìm đc a và b suy ra đa thức f(x) cần tìm.
Giải giùm nha!!
Câu hỏi của Bạch Quốc Huy - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.

Câu hỏi của Bạch Quốc Huy - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
f(x)= (x-3). Q(x)+2 moi X
f(x)=(x+4).H(x)+9 moi X
=>f(3)= 2
f( -4)= 9
f(x)= (x^2+x-12).(x^2+3)+ ax +b
=(x-3)(x+4). (x^2+3) +ax+b
=>f(3)= 3a+b=2
f(-4)=b -4a=9
=>a= -1; b=5
=> f(x)=(x^2+x-12)(x^2+3)-x+5
= x^4+x^3-9x^2+2x-31
# mui #

Bài 1:
\(2x^4+ax^2+bx+c⋮x-2\\ \Leftrightarrow2x^4+ax^2+bx+c=\left(x-2\right)\cdot a\left(x\right)\)
Thay \(x=2\Leftrightarrow32+4a+2b+c=0\Leftrightarrow4a+2b+c=-32\left(1\right)\)
\(2x^4+ax^2+bx+c:\left(x^2-1\right)R2x\\ \Leftrightarrow2x^4+ax^2+bx+c=\left(x-1\right)\left(x+1\right)\cdot b\left(x\right)+2x\)
Thay \(x=1\Leftrightarrow2+a+b+c=2\Leftrightarrow a+b+c=0\left(2\right)\)
Thay \(x=-1\Leftrightarrow2+a-b+c=-2\Leftrightarrow a-b+c=-4\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Leftrightarrow\left\{{}\begin{matrix}4a+2b+c=-32\\a+b+c=0\\a-b+c=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{34}{3}\\b=2\\c=\dfrac{28}{3}\end{matrix}\right.\)
Bài 2:
Do \(f\left(x\right):x^2+x-12\) được thương bậc 2 nên dư bậc 1
Gọi đa thức dư là \(ax+b\)
Vì \(f\left(x\right):x^2+x-12\) được thương là \(x^2+3\) và còn dư nên
\(f\left(x\right)=\left(x^2+x-12\right)\left(x^2+3\right)+ax+b\\ \Leftrightarrow f\left(x\right)=\left(x+4\right)\left(x-3\right)\left(x^2+3\right)+ax+b\)
Thay \(x=3\Leftrightarrow f\left(3\right)=3a+b\)
Mà \(f\left(x\right):\left(x-3\right)R2\Leftrightarrow f\left(3\right)=2\Leftrightarrow3a+b=2\left(1\right)\)
Thay \(x=-4\Leftrightarrow f\left(-4\right)=-4a+b\)
Mà \(f\left(x\right):\left(x+4\right)R9\Leftrightarrow f\left(-4\right)=9\Leftrightarrow-4a+b=-9\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}3a+b=2\\-4a+b=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=5\end{matrix}\right.\)
Do đó \(f\left(x\right)=\left(x^2+x-12\right)\left(x^2+3\right)-x+5\)
\(\Leftrightarrow f\left(x\right)=x^4+3x^2+x^3+3x-12x^2-36-x+5\\ \Leftrightarrow f\left(x\right)=x^4+x^3-9x^2+2x-31\)
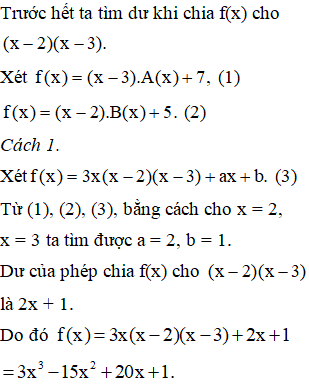
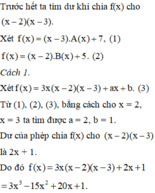
Chia f(x) cho x+1 thì dư 6 => \(f\left(x\right)-6⋮x+1\)
hay \(x^2+ax+b-6⋮x+1\)
Làm tính chia đa thức ta được: \(\left(x^2+ax+b-6\right):\left(x+1\right)=x-1+a\)
và dư ra \(b-a-5\)
Mà phép tính trên chia hết \(\Rightarrow b-a-5=0\Leftrightarrow b-a=5\)(1)
Tương tự: \(x^2+ax+b-3⋮x-2\)
Ta có: \(\left(x^2+ax+b-3\right):\left(x-2\right)=x+2+a\)
dư ra \(2a+b+1\). Phép chia chia hết \(\Leftrightarrow2a+b+1=0\Leftrightarrow2a+b=-1\)(2)
Từ (1) và (2) \(\Rightarrow2a+b-\left(b-a\right)=-1-5\)
\(\Leftrightarrow2a+b-b+a=-6\)
\(\Leftrightarrow3a=-6\Rightarrow a=-2\)
\(\Rightarrow b=3\)
Thay \(a=-2,b=3\)vào \(f\left(x\right):\)
\(f\left(x\right)=x^2-2x+3\)
Vậy...