PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
22 tháng 11 2017
Vì x 2 – 2x + 5 luôn luôn dương nên hàm số xác định trên (− ∞ ; + ∞ )
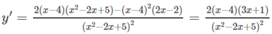
y′ = 0 ⇔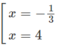 
Bảng biến thiên:
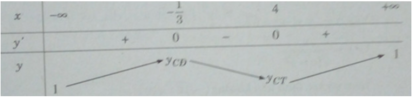
Hàm số đạt cực đại tại x = −1/3, đạt cực tiểu tại x = 4 và y CD = y(−1/3) = 13/4; y CT = y(4) = 0
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
Xét trên các miền xác định của các hàm (bạn tự tìm miền xác định)
a.
\(y'=\dfrac{1}{2\sqrt{x-3}}-\dfrac{1}{2\sqrt{6-x}}=\dfrac{\sqrt{6-x}-\sqrt{x-3}}{2\sqrt{\left(x-3\right)\left(6-x\right)}}\)
\(y'=0\Rightarrow6-x=x-3\Rightarrow x=\dfrac{9}{2}\)
\(x=\dfrac{9}{2}\) là điểm cực đại của hàm số
b.
\(y'=1-\dfrac{9}{\left(x-2\right)^2}=0\Rightarrow\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
\(x=-1\) là điểm cực đại, \(x=5\) là điểm cực tiểu
c.
\(y'=\sqrt{3-x}-\dfrac{x}{2\sqrt{3-x}}=0\Rightarrow2\left(3-x\right)-x=0\)
\(\Rightarrow x=2\)
\(x=2\) là điểm cực đại
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
d.
\(y'=\dfrac{-x^2+4}{\left(x^2+4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
\(x=-2\) là điểm cực tiểu, \(x=2\) là điểm cực đại
e.
\(y'=\dfrac{-8\left(x^2-5x+4\right)}{\left(x^2-4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
\(x=1\) là điểm cực tiểu, \(x=4\) là điểm cực đại
PT
1
CM
30 tháng 10 2019
TXĐ: R
y′ = 2(x + 2). x - 3 3 + 3 x + 2 2 . x - 3 2 = 5x(x + 2). x - 3 2
y′= 0 ⇔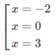 
Bảng biến thiên:
Từ đó suy ra y CĐ = y(-2) = 0; y CT = y(0) = -108.
PT
1
23 tháng 4 2016
Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm
15 tháng 12 2023
ĐKXĐ: \(2x-x^3>=0\)
=>\(x^3-2x< =0\)
=>\(\left[{}\begin{matrix}x< =-\sqrt{2}\\0< =x< =\sqrt{2}\end{matrix}\right.\)
\(y=\sqrt{2x-x^3}\)
=>\(y'=\dfrac{\left(2x-x^3\right)'}{2\cdot\sqrt{2x-x^3}}=\dfrac{2-3x^2}{2\cdot\sqrt{2x-x^3}}\)
Đặt y'=0
=>\(2-3x^2=0\)
=>\(3x^2=2\)
=>\(x^2=\dfrac{2}{3}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}}{3}\left(nhận\right)\\x=-\dfrac{\sqrt{6}}{3}\left(loại\right)\end{matrix}\right.\)
Khi \(x=\dfrac{\sqrt{6}}{3}\) thì \(y=\sqrt{2\cdot\dfrac{\sqrt{6}}{3}-\left(\dfrac{\sqrt{6}}{3}\right)^3}\)
\(=\sqrt{\dfrac{4\sqrt{6}}{9}}=\dfrac{2}{3}\cdot\sqrt{\sqrt{6}}\)
15 tháng 12 2023
https://hoc24.vn/cau-hoi/giai-cac-phuong-trinh-sau1-2x2-5x6-21-x2-2-26-5x-12-16sin2x-16cos2x-10.8680426955871
PT
1
CM
20 tháng 9 2019
TXĐ : R
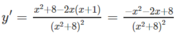
y′= 0 ⇔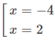 
Bảng biến thiên:
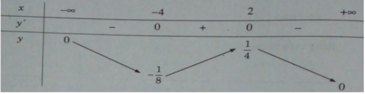
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = -4 và y CD = y(2) = 1/4; y CT = y(−4) = −1/8
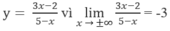
Hàm số xác định trên khoảng (− ∞ ;+ ∞ ).
Bảng biến thiên:
Vậy y CD = y(−2) =