Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

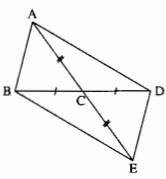
Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
A B C D E
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)


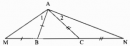
Ta có:
AB=AC(gt)(1);AM=12AB(gt)(2);AN=12AC(gt)(3)AB=AC(gt)(1);AM=12AB(gt)(2);AN=12AC(gt)(3)
Từ (1), (2) và (3) suy ra: AM = AN
Xét hai tam giác vuông AMI và ANI, ta có:
ˆAMI=ˆANI=90∘AMI^=ANI^=90∘
AM = AN (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆AMI = ∆ANI (cạnh huyền, cạnh góc vuông)
Suy ra ˆA1=ˆA2A1^=A2^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆBAC



Xét tam giác ABC,ta có:
AB=AC(theo hình vẽ)
góc BAC=90°(theo hình vẽ)
=>tam giác ABC vuông cân tại A
Nên: góc ABC=góc ACB
Mà: góc ABC+góc ACB=180°-góc BAC=180°-90°=90°
=>góc ABC=góc ACB=90°/2=45°
Mặt khác, ta lại có:
góc ABC+góc DBC=180°(2 góc kề bù)
=>góc DBC=180°-góc ABC=180°-45°=135°
Ta có: BD=BC(theo hình vẽ)
=>tam giác DBC cân tại B
=>góc BDC=góc BCD=45°/2=22,5°=góc ADC( vì A,B,D thẳng hàng)
=> góc ACD=góc ACB+góc BCD=45°+22,5°=67,5°.
Vậy các góc của tam giác ACD là:
góc CAD=90°
góc ACD=67,5°
góc ADC=22,5°





hình đâu
Phải cho hình chứ bạn!!