NT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
0
TT
10 tháng 5 2019
ĐỂ \(\frac{7}{2n-1}\) có gtri nguyên <=> 7 chia hết cho 2n-1
=>2n-1 thuộc tập hợp Ư(7)={7;1;-7;-1}
=>2n thuộc {8;2;-6;0}=>n thuộc {4;1;-3;0}
DH
1
18 tháng 2 2020
Để phân số :\(\frac{2n+3}{7}\) có giá trị là số nguyên thì 2n+3:7
\(\implies\) \(2n+3=7k\)
\(\implies\) 2n=7k-3
\(\implies\) n=\(\frac{7k-3}{2}\)
Vậy với mọi số nguyên n có dang \(\frac{7k-3}{2}\) thì phân số \(\frac{2n+3}{7}\) có giá trị là số nguyên
28 tháng 6 2023
a: 12/3n-1 là số nguyên khi 3n-1 thuộc Ư(12)
=>3n-1 thuộc {1;-1;2;-2;3;-3;4;-4;6;-6;12;-12}
mà n là số nguyên
nên n thuộc {0;1;-1}
c: 2n+5/n-3 là số nguyên
=>2n-6+11 chia hết cho n-3
=>n-3 thuộc {1;-1;11;-11}
=>n thuộc {4;2;14;-8}
NL
11 tháng 2 2020
a) Để phân số \(\frac{12}{3n-1}\)có giá trị là 1 số nguyên
\(\Rightarrow\)12\(⋮\)3n-1
\(\Rightarrow3n-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm12\right\}\)
Tiếp theo bạn tìm số nguyên n như thường, nếu có giá trị là phân số thì bỏ nên bạn tự làm nhé!
b) Để phân số \(\frac{2n+3}{7}\)có giá trị là 1 số nguyên
\(\Rightarrow\)2n+3\(⋮\)7
\(\Rightarrow\)2n+3=7k
\(\Rightarrow n=\frac{7k-3}{2}\)
2 tháng 3 2023
a: Để A là phân số thì n-2<>0
=>n<>2
Khi n=-2 thì \(A=\dfrac{2\cdot\left(-2\right)+1}{-2-2}=\dfrac{-3}{-4}=\dfrac{3}{4}\)
b: Để A nguyên thì 2n+1 chia hết cho n-2
=>2n-4+5 chia hết cho n-2
=>\(n-2\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{3;1;7;-3\right\}\)
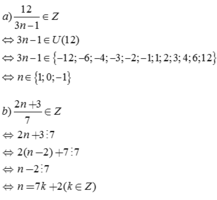
có số { 0;1 }
k mk nha ♥
Vì 7/2n-1 có giá trị là số nguyên
=> 7 chia hết cho 2n-1
=> 2n-1 thuộc ước của 7
Ư(7)={1;-1;7;-7}
Ta có bảng :
2n-1 1 -1 7 -7
2n 2 0 8 -6
n 1 0 4 -3
Vậy với n thuộc {-3;0;1;4} thì thỏa mãn đầu bài