Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S=x^2+y^2;\)\(\frac{x^3+y^3}{x+y}=T\)
\(\Rightarrow\left(x^2+y^2\right)-\frac{x^3+y^3}{x+y}=28\)
\(\Leftrightarrow x^2+y^2-\frac{\left(x+y\right)\left(x^2-xy+y^2\right)}{x+y}=28\)
\(\Leftrightarrow xy=28\)
Vì x,y nguyên và x<y nên ta xét từng trường hợp:
- \(\hept{\begin{cases}x=-28\\y=-1\end{cases}}\)
- \(\hept{\begin{cases}x=-14\\y=-2\end{cases}}\)
- \(\hept{\begin{cases}x=-7\\y=-4\end{cases}}\)
- \(\hept{\begin{cases}x=1\\y=28\end{cases}}\)
- \(\hept{\begin{cases}x=2\\y=14\end{cases}}\)
- \(\hept{\begin{cases}x=4\\y=7\end{cases}}\)
Ta được \(\left(x;y\right)=\left(-28;-1\right);\left(-14;-2\right);\left(-7;-4\right);\left(1;28\right);\left(2;14\right);\left(4;7\right)\)

gọi 2 số đó là a và b \(\left(a,b>0\right)\)
Theo đề: \(\left\{{}\begin{matrix}a+b=19\left(1\right)\\a^2+b^2=185\left(2\right)\end{matrix}\right.\)
Từ (1) \(\Rightarrow\left(a+b\right)^2=19^2=361\left(3\right)\)
Lấy \(\left(3\right)-\left(2\right)\Rightarrow2ab=176\Rightarrow ab=88\left(4\right)\)
Từ (1) và (4) \(\Rightarrow a,b\) là nghiệm của pt \(x^2-19x+88=0\)
\(\Rightarrow\left(x-11\right)\left(x-8\right)=0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=8\\b=11\end{matrix}\right.\\\left\{{}\begin{matrix}a=11\\b=8\end{matrix}\right.\end{matrix}\right.\)
Vậy 2 số cần tìm là 8 và 11


Vậy 2 số cần tìm là 8 và 11Gọi 2 số tự nhiên cần tìm là a,b (a>b)
Theo giả thiết, ta có
a + b = 19 và a^2 + b^2 = 185
=> 2ab = (a+b)^2 - (a^2+b^2) = 176 <=> ab = 88
=> a,b là nghiệm của pt x^2 - 19x + 88 = 0 (*)
(*) <=> (x-11)(x-8) = 0 <=> x= 8 hoặc x = 11
=> (a,b) = (11;8)
gọi x là số tự nhiên thứ nhất , y là số tự nhiên thứ hai . (x,y > 0)
tổng của chúng bằng 19
=> x + y = 19
<=> x = 19 - y
tổng các bình phương của chúng bằng 185
=> x^2 + y^2 = 185
<=> (19 - y)^2 + y^2 = 185
<=> 361 - 38y + y^2 + y^2= 185
<=> 2y^2 - 38y + 176 = 0
<=> y = 8 hoặc y = 11
y = 8 => x = 19 - 8 = 11
y = 11 => x = 19 - 11 = 8
vậy hai số tự nhiên đó là 8 và 11


Gọi số thứ nhất là x. Như vậy thì số thứ hai là 20-x.
Ta có phương trình \(x^2+\left(20-x\right)^2=280\Leftrightarrow2x^2-40x+120=0\Leftrightarrow x^2-20x+60=0\Rightarrow x=10\pm2\sqrt{10}\)
Vậy hai số đó là \(10+2\sqrt{10}\)và\(10-2\sqrt{10}\)

Gọi hai số cần tìm là x, y.
Theo đề bài ta có:
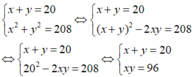
Suy ra x, y là nghiệm của phương trình:
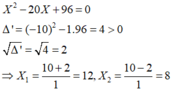
Vậy hai số cần tìm là 12 và 8
từ đề bài suy ra (a+b+c)^3=1suy ra (a^3)+(b^3)+(c^3)+3(a+b)(b+c)(c+a)=0 suy ra (a+b)(b+c)(c+a)=0 ( vì (a^3)+(b^3)+(c^3)=0)
nếu a+b=0 suy ra a= -b
lại có a+b+c=1 suy ra c=1
các TH còn lại CM tương tự