Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp giải:
Tìm tọa độ các điểm cực trị của hàm số trùng phương sau đó dựa vào tính chất của tứ giác nội tiếp đường tròn để tìm được tham số m
Lời giải:
Ta có



Đáp án B
Đồ thị hàm số có 3 điểm cực trị ⇔ y ' = 4 x 2 x 2 + m đổi dấu 3 lần ⇔ m < 0
Khi đó, gọi A 0 ; − 3 m 2 , B − m 2 ; − m 2 − 3 m 2 và C − − m 2 ; − m 2 − 3 m 2 là ba điểm cực trị
Vì y A > y B = y C nên yêu cầu bài toán ⇔ Tứ giác A B O C nội tiếp I
Vì A B = A C O B = O C → O A là đường trung trực của đoạn thẳng BC
Suy ra AO là đường kính của I = O B → . A B → = 0 ⇔ m 2 + m 2 2 . m 2 + 3 2 = 0 ⇔ m = − 1 m = − 1 − 3
Vậy tổng các giá trị của tham số m là − 2 − 3

Đáp án B
Đồ thị hàm số có 3 điểm cực trị ⇔ y ' = 4 x 2 x 2 + m đổi dấu 3 lần ⇔ m < 0
Khi đó, gọi A 0 ; − 3 m 2 , B − m 2 ; − m 2 − 3 m 2 và C − − m 2 ; − m 2 − 3 m 2 là 3 điểm cực trị
Vì y A > y B = y C nên yêu cầu bài toán
<=> Tứ giác ABOC nội tiếp (I)
Vì A B = A C O B = O C → O A là đường trung trực của đoạn thẳng BC
Suy ra OA là đường kính của (I)
=> I ⇒ O B → . A B → = 0 ⇔ − m 2 + m 2 2 . m 2 + 3 m 2 = 0 ⇔ m = − 1 m = − 1 − 3
Vậy tổng các giá trị của tham số m là − 2 − 3

Chọn B.
Phương pháp:
Sử dụng dấu hiệu nhận biết của tứ giác nội tiếp.
Cách giải:
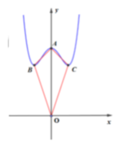


Khi đó,
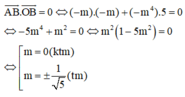
Vậy tập hợp S tất cả các giá trị của tham số m thỏa mãn yêu cầu đề bài có 2 phần tử là ± 1 5 .
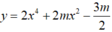 có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.
có ba điểm cực trị, đồng thời ba điểm cực trị này cùng với gốc tọa độ O tạo thành bốn đỉnh của một tứ giác nội tiếp được. Tính tổng tất cả các phần tử của S.


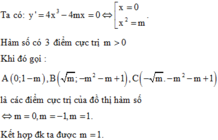
Phương pháp:
+) Tìm tọa độ các điểm cực trị của đồ thị hàm số theo tham số m.
+) Dựa vào tính chất hàm trùng phương và tính chất tứ giác nội tiếp để tìm m.
Cách giải: