Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Áp dụng quy tắc L'Hopital
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+1}-1}{f\left(0\right)-f\left(x\right)}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{1}{2\sqrt{x+1}}}{-f'\left(0\right)}=-\dfrac{1}{6}\)
2.
\(g'\left(x\right)=2x.f'\left(\sqrt{x^2+4}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(\sqrt{x^2+4}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\sqrt{x^2+4}=1\\\sqrt{x^2+4}=-2\end{matrix}\right.\)
2 pt cuối đều vô nghiệm nên \(g'\left(x\right)=0\) có đúng 1 nghiệm

Do \(x< 2\) nên x chỉ tiến tới 2 từ phía trái
Do đó hàm số chỉ có giới hạn trái tại điểm x=2 (giới hạn bằng dương vô cực)

Chọn C.
Ta có:
lim x → 2 + f ( x ) = lim x → 2 + ( x 2 + a x + 2 ) = 2 a + 6 .
lim x → 2 − f ( x ) = lim x → 2 − ( 2 x 2 − x + 1 ) = 7 .
Hàm số có giới hạn khi x → 2 ⇔ lim x → 2 + f ( x ) = lim x → 2 − f ( x ) ⇔ 2 a + 6 = 7 ⇔ a = 1 2 .
Vậy a = 1 2 là giá trị cần tìm.

a) Với x bất kì và \(h = x - {x_0}\), ta có:
\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {{x_0} + h} \right) - f\left( {{x_0}} \right)}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{{{e^{{x_0} + h}} - {e^{{x_0}}}}}{h}\\ = \mathop {\lim }\limits_{h \to 0} \frac{{{e^{{x_o}}}\left( {{e^h} - 1} \right)}}{h} = \mathop {\lim }\limits_{h \to 0} {e^{{x_0}}}.\mathop {\lim }\limits_{h \to 0} \frac{{{e^h} - 1}}{h} = {e^{{x_0}}}\end{array}\)
Vậy hàm số \(y = {e^x}\) có đạo hàm là hàm số \(y' = {e^x}\)
b) Ta có \({a^x} = {e^{x\ln a}}\,\)nên \(\left( {{a^x}} \right)' = \left( {{e^{x\ln a}}} \right)' = \left( {x\ln a} \right)'.{e^{x\ln a}} = {e^{x\ln a}}\ln a = {a^x}\ln a\)

Với a = 0, b = 1, hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + 1}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + 1} \right) = - 3.2 + 1 = - 5\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x} \right) = 2.2 = 4\\ \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\end{array}\)
Do đó không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\)
Vậy hàm số không liên tục tại x = 2.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + b} \right) = - 3.2 + b = - 6 + b\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + a} \right) = 2.2 + a = 4 + a\\f\left( 2 \right) = 4\end{array}\)
Để hàm số liên tục tại x = 2 thì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\)
\( \Leftrightarrow - 6 + b = 4 + a = 4 \Leftrightarrow \left\{ \begin{array}{l}4 + a = 4\\ - 6 + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 10\end{array} \right.\)
Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.
c) Tập xác định của hàm số là: ℝ.
Với x < 2 thì \(f\left( x \right) = 2x + a\) là hàm đa thức nên liên tục.
Với x > 2 thì \(f\left( x \right) = -3x + b\) là hàm đa thức nên liên tục.
Do đó để hàm số liên tục trên ℝ thì hàm số \(f\left( x \right)\) liên tục tại x = 2.
Vậy với a = 0 và b = 10 thỏa mãn điều kiện.

Lời giải:
Để hàm số trên liên tục tại $x_0=0$ thì:
\(\lim\limits_{x\to 0+}f(x)=\lim\limits_{x\to 0-}f(x)=f(0)\)
\(\Leftrightarrow \lim\limits_{x\to 0+}(a+\frac{4-x}{x+2})=\lim\limits_{x\to 0-}(\frac{\sqrt{1-x}+\sqrt{1+x}}{x})=a+2\)
\(\Leftrightarrow a+2=\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}\)
Mà \(\lim\limits_{x\to 0-}\frac{\sqrt{1-x}+\sqrt{1+x}}{x}=-\infty \) nên không tồn tại $a$ để hàm số liên tục tại $x_0=0$
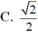
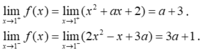
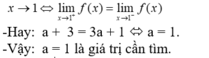
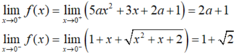
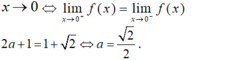
Chọn C.
Ta có: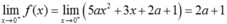
Vậy