K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LD
2
29 tháng 1 2018
Ta có : (20 + 25 + a + b + 24)/5 = 25
=> 20 + 25 + a + b + 24 = 25 . 5 = 125
=> 69 + a + b = 125
=> a + b = 125 - 69 = 56
a/6 = b/8 = (a + b)/(6 + 8) = 56/14 = 4 (tính chất dãy tỉ số bằng nhau)
=> a = 4 . 6 = 24
b = 4 . 8 = 32
29 tháng 1 2018
Ta có : (20 + 25 + a + b + 24)/5 = 25
=> 20 + 25 + a + b + 24 = 25 . 5 = 125
=> 9 + a + b = 125
=> a + b = 125 - 69 = 56
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{6}=\dfrac{b}{8}=\dfrac{a+b}{6+8}=\dfrac{56}{14}=4\)
=> a = 4 . 6 = 24
b = 4 . 8 = 32
TM
3
MH
13 tháng 2 2016
Ta có: (20 + 25 + a + a + 24) : 5 = 25
=> 20 + 25 + a + a + 24 = 25 x 5
=> 69 + 2a = 125
=> 2a = 125 - 69
=> 2a = 56
=> a = 56 : 2 = 28
NB
1
19 tháng 2 2022
Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{a+b+24+32}{4}=29\\a=2b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3b+56=116\\a=2b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\a=40\end{matrix}\right.\)
NL
0
16 tháng 3 2016
969
lấy 324 x 4 được 1296, lấy 1296 trừ cho 327 ra 969, ko tin bấm máy tính : (327 + 969) :4 xem đi .___.
HD
1
KN
31 tháng 1 2019
\(\hept{\begin{cases}2a+3b+2c=5\\5a+4b+c=55\\a+b-4c=24\end{cases}}\Leftrightarrow8a+8b-c=5+55+24\)
\(\Leftrightarrow8a+8b-c=84\)
\(\Leftrightarrow8\left(a+b\right)-c=84\)
\(\Leftrightarrow8\left(a+b\right)=84+c\)
\(\Rightarrow a+b+c=84\)
\(\Rightarrow TBC\left(a,b,c\right)=\frac{84}{3}=28\)
CM
8 tháng 11 2019
Tìm cách giải
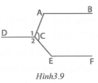
Trong hình vẽ đã có các cặp góc so le trong là A ^ và C 1 ^ ; E ^ và C 2 ^ . Muốn chứng tỏ AB // CD và CD // EF chỉ cần chứng tỏ A ^ = C 1 ^ và E ^ = C 2 ^ .
Trình bày lời giải
Ta có A C E ^ = C 1 ^ + C 2 ^ 2 ⇒ C 1 ^ + C 2 ^ = 2 A C E ^ .
Mặt khác C 1 ^ + C 2 ^ + A C E ^ = 360 ° nên 2 A C E ^ + A C E ^ = 360 ° ⇒ A C E ^ = 120 ° .
Do đó C 1 ^ + C 2 ^ = 360 ° − 120 ° = 240 ° mà C 1 ^ − C 2 ^ = 20 ° nên C 1 ^ = 130 ° ; C 2 ^ = 110 ° .
Ta có A C E ^ = A ^ + E ^ 2 ⇒ A ^ + E ^ = 2 A C E ^ = 240 ° .
Lại có A ^ − E ^ = 20 ° nên A ^ = 130 ° ; E ^ = 110 ° .
Ta có A ^ = C 1 ^ = 130 ° ⇒ A B / / C D ; E ^ = C 2 ^ = 110 ° ⇒ C D / / E F vì có cặp góc so le trong bằng nhau.
Vận dụng cặp góc đồng vị
KN
0
ta có: (20+25+a+a+24) = 25.5
(79+2a) = 125
2a = 125 - 79
2a = 46
a = 23
ta có:
(20 + 25 + a + a + 24) = 25.5
(69 + 2a) = 125
2a = 125-69
2a = 56
a = 28
Cái dưới sai bạn nhé