Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đăng từng bài thôi nha bạn
Bài 1 :
\(A=\left(2x-1\right)^2+2\left(2x-1\right)\left(2x+1\right)+\left(2x+1\right)^2\)
\(A=\left(2x-1+2x+1\right)^2\)
\(A=\left(4x\right)^2\)
\(A=16x^2\)
Câu B mình không hiểu đề cho lắm
Bài 2 :
\(a)\) \(\left(x-1\right)\left(x+1\right)-\left(x+1\right)^2=4\)
\(\Leftrightarrow\)\(x^2-1-\left(x+1\right)^2=4\)
\(\Leftrightarrow\)\(\left(x-x-1\right)\left(x+x+1\right)=4+1\)
\(\Leftrightarrow\)\(\left(-1\right)\left(2x+1\right)=5\)
\(\Leftrightarrow\)\(2x+1=-5\)
\(\Leftrightarrow\)\(2x=-6\)
\(\Leftrightarrow\)\(x=-3\)
Vậy \(x=-3\)
Chúc bạn học tốt ~

a: \(=y^2-9\)
b: \(=m^3+n^3\)
c: \(=8-a^3\)
d: \(=\left(a-b-c-a+b-c\right)\left(a-b-c+a-b+c\right)\)
\(=-2c\cdot\left(2a-2b\right)\)
\(=-4ac+4bc\)
f: \(=\left(1-x^3\right)\left(1+x^3\right)=1-x^6\)

\(1,Q=\dfrac{a^4-2a^2+a^3-2a+a^2-2}{a^4-2a^2+2a^3-4a+a^2-2}\\ Q=\dfrac{\left(a^2-2\right)\left(a^2+a+1\right)}{\left(a^2-2\right)\left(a^2+2a+1\right)}=\dfrac{a^2+a+1}{a^2+2a+1}\)
\(Q=\dfrac{x^2+x+1}{\left(x+1\right)^2}-\dfrac{3}{4}+\dfrac{3}{4}=\dfrac{x^2+x+1-\dfrac{3}{4}x^2-\dfrac{3}{2}x-\dfrac{3}{4}}{\left(x+1\right)^2}+\dfrac{3}{4}\\ Q=\dfrac{\dfrac{1}{4}x^2-\dfrac{1}{2}x+\dfrac{1}{4}}{\left(x+1\right)^2}+\dfrac{3}{4}=\dfrac{\dfrac{1}{4}\left(x-1\right)^2}{\left(x+1\right)^2}+\dfrac{3}{4}\ge\dfrac{3}{4}\\ Q_{min}=\dfrac{3}{4}\Leftrightarrow x=1\)
\(2,\text{Từ GT }\Leftrightarrow\dfrac{ayz+bxz+czy}{xyz}=0\\ \Leftrightarrow ayz+bxz+czy=0\\ \text{Ta có }\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\\ \Leftrightarrow\left(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}\right)^2=1\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\left(\dfrac{xy}{ab}+\dfrac{yz}{bc}+\dfrac{zx}{ca}\right)=0\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\cdot\dfrac{cxy+ayz+bzx}{abc}=1\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}+2\cdot\dfrac{0}{abc}=1\\ \Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\)
Mà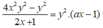 nên a = 2
nên a = 2
Chọn đáp án A