Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta co: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a-b}{c-d}\)
\(\Rightarrow\frac{a}{a-b}=\frac{c}{c-d}\)
b) Ta co: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow\frac{a+c}{b+d}=\frac{a}{b}\)
a) x:y:z=2:3:4
\(\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
\(\Rightarrow\frac{x^2}{4}=\frac{2y^2}{18}=\frac{z^2}{16}=\frac{x^2+2y^2-z^2}{4+18-16}=\frac{24}{6}=4\) (Theo t/c dãy tỉ số bằng nhau)
\(\Rightarrow\frac{x^2}{4}=4\Rightarrow x=4\)
\(\frac{2y^2}{18}=4\Rightarrow y=6\)
\(\frac{z^2}{16}=4\Rightarrow z=8\)
Câu b) cũng tương tự vậy:
-Lập tỉ số theo đề.
-Áp dụng t/c DTSBN.
-Tìm x,y,z,t theo tỉ số.
câu 1 bạn bình giải
câu 2
ta có x:y:z:t=2:3:4:5 và x+y+z+t=-42
=> \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{t}{5}\) và x+y+z+t=-42
áp dụng tính chất dãy tỉ số bằng nhau,ta có
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{t}{5}=\frac{x+y+z+t}{2+3+4+5}=-\frac{42}{14}=-3\)
*\(\frac{x}{2}=-3=>x=-3.2=-6\)
*\(\frac{y}{3}=-3=>y=-3.3=-9\)
*\(\frac{z}{4}=-3=>z=-3.4=-12\)
*\(\frac{t}{5}=-3=>t=-3.5=-15\)
vậy \(x=-6;y=-9;z=-12;t=-15\)
Vì f(x)=ax2+b mà f(0)=3 nên f(0)=a.0+b=3 => f(0)=b=3
Vì f(x)=ax2+b mà f(-2)=-9 nên f(-2)=a.(-2)2+b=-9=>a.4+b=-9 Thay b= 3 ta được :a.4+3=-9=>a.4=-12=>a=-3
Vậy b=3 ;a=-3
nhớ k
C1: a)Vì OA=OB
=>tam giác AOB cân tại O
Xét tam giác ABO có OI là tia phân giác đồng thời là đường cao
=>OI vuông góc với AB
b)
Xét tam giác OAC và tam giác OBC có:
OA=OB(gt)
góc AOC= góc BOC(OC là tia phân giác góc AOB
OC chung
=> tam giác AOC= tam giác BOC(c-c-c)
=>\(\widehat{OAC}=\widehat{OBC}=90độ\)(2 góc tương ứng)
Vậy BC vuông góc với Oy
C2:
a)Xét tam giác OAI và tam giác OBI có:
OA=OB
góc AOI=gócBOI(OI là tia phân giác góc AOB)
=>góc OIA= góc OIB=90độ(2 góc tương ứng)
=>OI vuông góc với BC
b)Xét tam giác AOC và tam giác BOC có:
OA=OB(gt)
góc AOC = góc BOC(OC là tia phân giác góc AOB)
OC chung
=>tam giác AOC=tam giác BOC(c-g-c)
=>góc OAC= góc OBC=90độ(2 góc tương ứng)
=>BC vuông góc với Oy
Nếu bạn học xong lớp 7 rồi thì làm cách 1 còn nếu bạn mới học lớp 7 thì làm theo cách 2 để giải chi tiết
quá đơn giản
cho 5 k giải cho
(mình trong đội tuyển toán đó nhe nên làm theo đi)
a) Ta có :\(\left(x+2\right)^2\ge0;\left(y-4\right)^4\ge0;Với\forall x,y\in Z\)
\(\Rightarrow\orbr{\begin{cases}\left(x+2\right)^2=0\\\left(y-3\right)^4=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x+2=0\\y-3=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-2\\y=3\end{cases}}\)
Vậy để (x+2)2 + (y-4)4 =0 thì x = -2 và y = 3
b)Ta có :\(\left(x+y-11\right)^2\ge0;\left(x-y-4\right)^2\ge0;Với\forall x,y\in Z\)
\(\Rightarrow\orbr{\begin{cases}\left(x+y-11\right)^2=0\\\left(x-y-4\right)^2=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x+y=11\\x-y=4\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\left(11+4\right):2=7,5\\y=\left(11-4\right):2=3,5\end{cases}}\)
Vậy để (x+y-11)2 + (x-y-4)2=0 thì x = 7,5 và y = 3,5
a) Ta có :(x+2)2≥0;(y−4)4≥0;Với∀x,y∈Z
⇒[
| (x+2)2=0 |
| (y−3)4=0 |
⇒[
| x+2=0 |
| y−3=0 |
⇒[
| x=−2 |
| y=3 |
Vậy để (x+2)2 + (y-4)4 =0 thì x = -2 và y = 3
b)Ta có :(x+y−11)2≥0;(x−y−4)2≥0;Với∀x,y∈Z
⇒[
| (x+y−11)2=0 |
| (x−y−4)2=0 |
⇒[
| x+y=11 |
| x−y=4 |
⇒[
| x=(11+4):2=7,5 |
| y=(11−4):2=3,5 |
Vậy để (x+y-11)2 + (x-y-4)2=0 thì x = 7,5 và y = 3,5
Do \(\left|0,2x-3,1\right|\ge0\); \(\left|0,2x+3,1\right|\ge0\)
=> \(\left|0,2x-3,1\right|+\left|0,2x+3,1\right|\ge0\)
Mà theo đề bài: |0,2x - 3,1| + |0,2x + 3,1| = 0
=> \(\begin{cases}\left|0,2x-3,1\right|=0\\\left|0,2x+3,1\right|=0\end{cases}\)=> \(\begin{cases}0,2x-3,1=0\\0,2x+3,1=0\end{cases}\)=> \(\begin{cases}0,2x=3,1\\0,2x-3,1\end{cases}\), vô lý
Vì 0,2x = 0,2x; \(3,1\ne-3,1\)
Vậy không tồn tại giá trị của x thỏa mãn đề bài
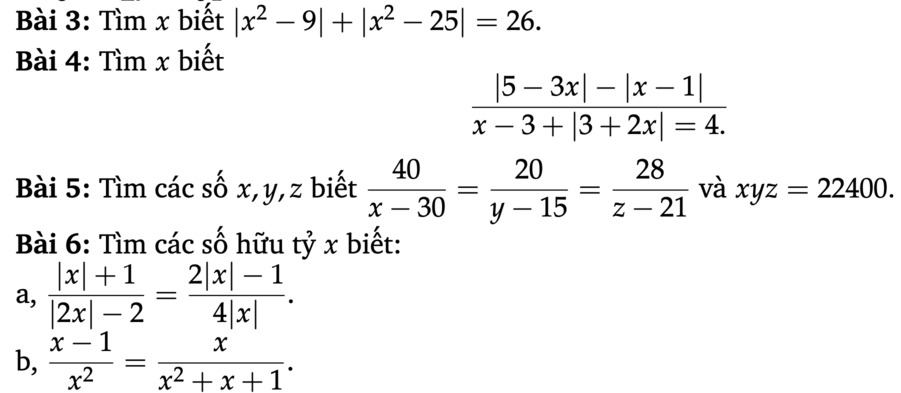(mình sẽ tích cho tất cả các bạn)
ta có \(a^2+2ab-5=0\)
<=>\(a\left(a+2b\right)=5\)
vì a,b tuộc Z nên a,(a+2b) thuộc ước của 5...
em tự giải tiếp nhé
a2+2ab-5=0
<=>a2+2ab=5
<=>a(a=2b)=5
<=>a=1 và a+2b=5 / a=-1 và a+2b=-5 / a=5 và a+2b=1 / a=-5 và a+2b=-1
Bn tự giải tiếp nha! Mk lom đại đại thôi