Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài cạnh góc vuông lớn là x (m) x>100
Độ dài cạnh góc vuông nhỏ là x - 100(m)
Diện tích đảo lúc đầu là: \(\dfrac{x\left(x-100\right)}{2}\) m2
Diện tích đảo lúc sau là: \(\dfrac{x\left(x-100+50\right)}{2}=\dfrac{x\left(x-50\right)}{2}\) m2
Theo đề ra ta có pt:
\(\dfrac{x\left(x-100\right)}{2}+15000=\dfrac{x\left(x-50\right)}{2}\)
\(\Leftrightarrow\dfrac{x^2-100x}{2}+\dfrac{30000}{2}=\dfrac{x^2-50x}{2}\)
\(\Leftrightarrow x^2-100x+30000-x^2+50x=0\)
\(\Leftrightarrow-50x+30000=0\)
\(\Leftrightarrow50x=30000\)
\(\Leftrightarrow x=600\) (nhận)
Suy ra độ dài cạnh góc vuông lớn là 600 m
Độ dài cạnh góc vuông nhỏ là: 600 - 100 = 500 m
Diện tích đảo lúc đầu là: \(\dfrac{600.500}{2}=150000\) m2
= 150 km2

Gọi độ dài cạnh góc vuông nhỏ là x (m)(x > 0)
Độ dài cạnh góc vuông lớn là x + 8 (m)
Khi tăng độ dài cạnh góc vuông nhỏ lên 2 lần ta được cạnh có độ dài 2x (m)
Khi giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được cạnh có độ dài 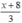 (m)
(m)
Tam giác vuông mới có diện tích bằng 51 m 2
Theo công thức tính diện tích tam giác vuông ta có phương trình:
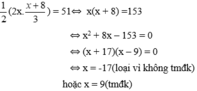
Vậy độ dài cạnh góc vuông nhỏ là 9m. Độ dài cạnh góc vuông lớn là 17m.

gọi \(x\) là độ dài cạnh góc vuông bé hơn \((x>0)\)
cạnh góc vuông lớn hơn là \(\frac{4x}{3}\)
diện tích tam giác vuông ban đầu là \((x\times\frac{4x}{3})\div2=\frac{2x^2}{3}\)
theo đề ra ta có phương trình
\((\frac{4x}{3}-2)\times x=\frac{2x^2}{3}\times75\div100\)
giải phương trình ta được \(\orbr{\begin{cases}x=0(ktm)\\x=2,4\end{cases}}\)