Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số lớn và số bé lần lượt là a,b(Điều kiện: \(a,b\in Z^+\))
Vì tỉ số của hai số là 3:4 nên ta có: a:b=4:3
hay \(a=\dfrac{4}{3}b\)
\(\Leftrightarrow a-\dfrac{4}{3}b=0\)(1)
Vì khi giảm số lớn đi 100 và tăng số nhỏ thêm 200 thì tỉ số mới là 5:3 nên ta có:
\(\dfrac{a-100}{b+200}=\dfrac{3}{5}\)
\(\Leftrightarrow5\left(a-100\right)=3\left(b+200\right)\)
\(\Leftrightarrow5a-500=3b+600\)
\(\Leftrightarrow5a-3b=1100\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a-\dfrac{4}{3}b=0\\5a-3b=1100\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a-\dfrac{20}{3}b=0\\5a-3b=1100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{11}{3}b=-1100\\a-\dfrac{4}{3}b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=300\\a-400=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=400\\b=300\end{matrix}\right.\)(thỏa ĐK)
Vậy: Số lớn là 400

Câu 2:
Gọi số phải tìm là ab
Vì tổng các chữ số của số cần tìm là 9 nên a+b=9(1)
Vì khi thêm vào số đó 63 đơn vị thì số thu được cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại nên \(10a+b+63=10b+a\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=9\\10a+b+63=10b+a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\10a+b+63-10b-a=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\9a-9b=-63\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\a-b=-7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\9-b-b=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=9-b\\-2b=-16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=9-8=1\\b=8\end{matrix}\right.\)
Vậy: Số cần tìm là 18

- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
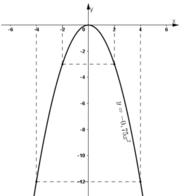
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = - 0 , 75 x 2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
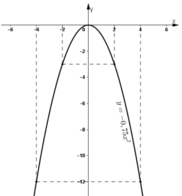
- Quan sát đồ thị hàm số y = - 0 , 75 x 2 :
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.

Gọi tử là: x
mẫu là: y\(\left(y\ne0\right)\)
\(\Rightarrow x+y=32\left(1\right)\)
Vì khi tăng mẫu thêm 10 đơn vị và giảm tử đi 1 nửa thì được phân số mới bằng \(\frac{2}{17}\)
\(\Rightarrow\frac{x.0,5}{y+10}=\frac{2}{17}\Leftrightarrow8,5x-2y=20\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\hept{\begin{cases}x+y=32\\8,5x-2y=20\end{cases}\Leftrightarrow\hept{\begin{cases}x=8\\y=24\end{cases}}}\)
\(\Rightarrow\)Phân số cằn tìm là: \(\frac{8}{24}=\frac{1}{3}\)

Vẽ đồ thị: y = -0,75x2
| x | -4 | -2 | -1 | 0 | 1 | 2 | 4 |
| y=-0,75x2 | -12 | -3 | -0,75 | 0 | -0,75 | -3 | -12 |
Vì -2 < 0 < 4 và khi x = 0 thì y = 0 là giá trị lớn nhất của hàm số. Hơn nữa khi x = -2 thì y = -0,75 . (-2)2 = -3, khi x = 4 thì y = -0,75 . (4)2 = -12 < -3
Do đó khi -2 ≤ x ≤ 4 thì giá trị nhỏ nhất của hàm số là -12 còn giá trị lớn nhất là 0.