Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Những đường thẳng song song với mặt phẳng (ABKI) là A’B’; D’C’; DC; GH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') mà A’D’ nằm trong mặt phẳng (A’D’C’B’) nên (A'B'C'D') ⊥ (CDD'C')

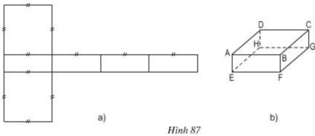
1. Gấp hình 33.a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật.
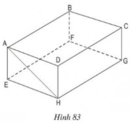
2. a) Trong hình hộp ABCD.EFGH thì:
+) BF vuông góc với hai đường thẳng cắt nhau EF và FG của mặt phẳng (EFGH) nên BF vuông góc với mặt phẳng (EFGH).
+) BF vuông góc với hai đường thẳng cắt nhau AB và BC của mặt phẳng (ABCD) nên BF vuông góc với mặt phẳng (ABCD).
b) Hai mặt phẳng (AEHD) và (CGHD)vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD).

a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

a) BC // FG ⇒ BC // (EFGH)
CD // HG ⇒ CD // (EFGH)
AD // EH ⇒ AD // (EFGH)
Vậy: ngoài AB, các cạnh song song với mặt phẳng (EFGH) là BC, CD, AD
b) CD // AB ⇒ CD // (ABFE)
và CD // (EFGH) ( theo ý a).
c) Vì AB // HG, AB = HG ⇒ ABGH là hình bình hành
⇒ AH // BG
⇒ AH // (BCGF)
Vậy mặt phẳng song song với đường thẳng AH là mặt phẳng (BCGF).

1. Gấp hình 33a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật
2. a) Trong hình hộp ABCD.EFGH thì:
BF song song với mp (DHGC) và mp (DHEA).
b) Hai mặt phẳng (AEHD) và (CGHD) vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông

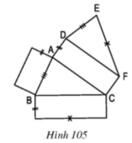
a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.
b) Các phát biểu đúng:
- Cạnh AD vuông góc với cạnh AB.
- EF và CF là hai cạnh vuông góc với nhau.
- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.

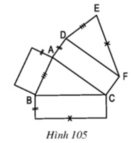
a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.
b) Các phát biểu đúng:
- Cạnh AD vuông góc với cạnh AB.
- EF và CF là hai cạnh vuông góc với nhau.
- Hai đáy (ABC) và (DEF) nằm trên hai mặt phẳng song song với nhau.
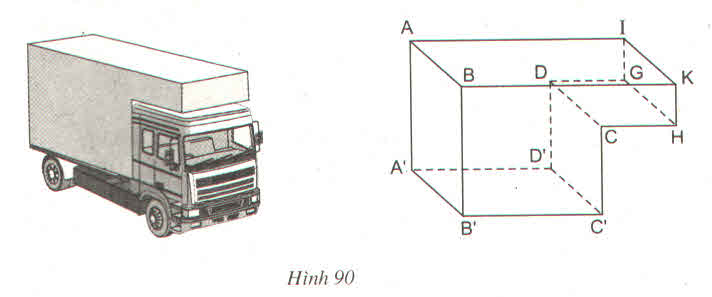
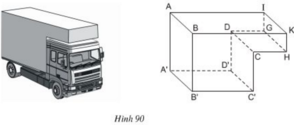
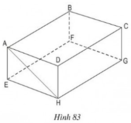
a) Những đường thẳng song song với mặt phẳng (ABKI) là DG; CH; A'D'; B'C'; A'B'; D'C'; DC; JH.
b) Những đường thẳng vuông góc với mặt phẳng (DCC'D') là A'D'; B'C'; DG; CH; AI; BK.
c) Ta có: A'D' ⊥ (CDD'C') => (A'B'C'D') \(\perp\) (CDD'C')
a) Những đường thẳng song song với mặt phẳng (ABKI) là : A’B’; D’C’; DC; JH
b) Những đường thẳng vuông góc với mặt phẳng (DCC’D’) là : A’D’; B’C’DJ; CH; AI; BK
c) Hai mặt phẳng (A’B’C’D’) và (CDD’C’) vuông góc với nhau