K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
2
LP
21 tháng 12 2021
\(=\dfrac{3}{2\left(x+3\right)}+\dfrac{6-x}{2x\left(x+3\right)}=\dfrac{3x+6-x}{2x\left(x+3\right)}=\dfrac{2x+6}{2x\left(x+6\right)}=\dfrac{2\left(x+3\right)}{2x\left(x+3\right)}=\dfrac{1}{x}\)
21 tháng 12 2021
\(=\dfrac{3x+6-x}{2x\left(x+3\right)}=\dfrac{2x+6}{2x\left(x+3\right)}=\dfrac{1}{x}\)
HP
6 tháng 9 2021
2.
\(\left(\dfrac{a}{b^2}+\dfrac{1}{a}-\dfrac{1}{b}\right):\left(\dfrac{b}{a}+\dfrac{a^2}{b^2}\right)\)
\(=\left(\dfrac{a^2}{ab^2}+\dfrac{b^2}{ab^2}-\dfrac{ab}{ab^2}\right):\left(\dfrac{b^3}{ab^2}+\dfrac{a^3}{ab^2}\right)\)
\(=\dfrac{a^2+b^2-ab}{ab^2}:\dfrac{\left(a+b\right)\left(a^2+b^2-ab\right)}{ab^2}\)
\(=\dfrac{a^2+b^2-ab}{ab^2}.\dfrac{ab^2}{\left(a+b\right)\left(a^2+b^2-ab\right)}\)
\(=\dfrac{1}{a+b}\)
HP
6 tháng 9 2021
1.
\(\left(a-\dfrac{x^2+a^2}{x+a}\right)\left(\dfrac{2a}{x}-\dfrac{4a}{x-a}\right)\)
\(=\dfrac{ax+a^2-x^2-a^2}{x+a}.\dfrac{2ax-2a^2-4ax}{x\left(x-a\right)}\)
\(=\dfrac{ax-x^2}{x+a}.\dfrac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}.\dfrac{2a\left(x+a\right)}{x\left(x-a\right)}\)
\(=2a\)
31 tháng 8 2021
\(a,\dfrac{6x-3}{5x^2+x}\cdot\dfrac{25x^2+10x+1}{1-8x^3}\\ =\dfrac{3\left(2x-1\right)}{x\left(5x+1\right)}\cdot\dfrac{\left(5x+1\right)^2}{\left(1-2x\right)\left(1+2x+4x^2\right)}\\ =\dfrac{-3\left(5x+1\right)}{x\left(1+2x+4x^2\right)}\)
\(b,\dfrac{x+3}{x^2-4}\cdot\dfrac{8-12x+6x^2-x^3}{9x+27}\\ =\dfrac{x+3}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(2-x\right)^3}{9\left(x+3\right)}\\ =\dfrac{-\left(2-x\right)^2}{9\left(x+2\right)}\)
\(c,\dfrac{x^2+5x+6}{x^2+7x+12}:\dfrac{x^2-4x+4}{x^2+3x}\\ =\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+3\right)\left(x+4\right)}\cdot\dfrac{x\left(x+3\right)}{\left(x-2\right)^2}\\ =\dfrac{x\left(x+2\right)\left(x+3\right)}{\left(x+4\right)\left(x-2\right)^2}\)
\(d,\dfrac{4a+6b}{a-1}:\dfrac{4a+12ab+9b^2}{1-a^3}\\ =\dfrac{2\left(2a+3b\right)}{a-1}\cdot\dfrac{\left(1-a\right)\left(a^2+a+1\right)}{\left(2a+3b\right)^2}\\ =\dfrac{-2\left(a^2+a+1\right)}{2a+3b}\)
\(e,\dfrac{x^2+2x-3}{x^2+3x-10}=\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x-2\right)\left(x+5\right)}\)
CD
6 tháng 12 2021
= x2 -9 - (x2 -x + 5x-5) - (x2 -8x +16)
= x2 -9 -x2 -4x +5 -x2 +8x-16
= -x2 +4x -20
Chẳng bik đề bài bảo j nên mình rút gọn nha!
9 tháng 12 2021
\(=\dfrac{4-6x+x^2+2x}{2\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-2\right)^2}{2\left(x-2\right)\left(x+2\right)}=\dfrac{x-2}{2\left(x+2\right)}\)
1 tháng 12 2021
\(4,\dfrac{11x}{2x-3}-\dfrac{18-x}{2x-3}=\dfrac{11x-18+x}{2x-3}=\dfrac{12x-18}{2x-3}=\dfrac{6\left(2x-3\right)}{2x-3}=6\\ 5,\dfrac{2x^3-x}{x-1}+\dfrac{x^3+3}{1-x}+\dfrac{2+x}{x-1}=\dfrac{2x^3-x+2+x}{x-1}-\dfrac{x^3+3}{x-1}=\dfrac{2x^3-x+2+x-x^3-3}{x-1}=\dfrac{x^3-1}{x-1}=\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x-1}=x^2+x+1\)
13 tháng 12 2021
\(=\dfrac{x+9-4x+x-3}{x\left(x-3\right)}=\dfrac{-2x+6}{x\left(x-3\right)}=\dfrac{-2\left(x-3\right)}{x\left(x-3\right)}=-\dfrac{2}{x}\)
U
13 tháng 12 2021
\(\dfrac{1}{x-3}+\dfrac{9-4x}{x^2-3x}+\dfrac{1}{x}=\dfrac{1}{x-3}+\dfrac{9-4x}{x\left(x-3\right)}+\dfrac{1}{x}=\dfrac{x}{x\left(x-3\right)}+\dfrac{9-4x}{x\left(x-3\right)}+\dfrac{x-3}{x\left(x-3\right)}=\dfrac{x+9-4x-x+3}{x\left(x-3\right)}=\dfrac{-4x+12}{x\left(x-3\right)}=\dfrac{-4\left(x-3\right)}{x\left(x-3\right)}=\dfrac{-4}{x}\)
22 tháng 12 2021
\(=x^2+1-\dfrac{x^4-3x^2-x^2+3}{x^2-1}\\ =x^2+1-\dfrac{\left(x^2-3\right)\left(x^2-1\right)}{x^2-1}\\ =x^2+1-x^2+3=4\)
6 tháng 1 2022
a: \(=\dfrac{4x^2\cdot5y}{5y^2\cdot6x}=\dfrac{2x}{3}\cdot\dfrac{1}{y}=\dfrac{2x}{3y}\)
b: \(=\dfrac{x^2-2x+1}{x\left(x-1\right)}=\dfrac{x-1}{x}\)
29 tháng 12 2021
10: \(=\dfrac{5x+20+4x-16-2x+24}{\left(x-4\right)\left(x+4\right)}=\dfrac{7x+28}{\left(x-4\right)\left(x+4\right)}=\dfrac{7}{x-4}\)
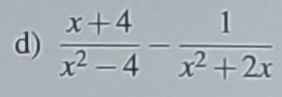
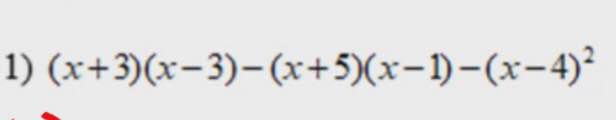
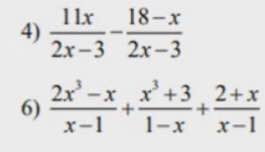
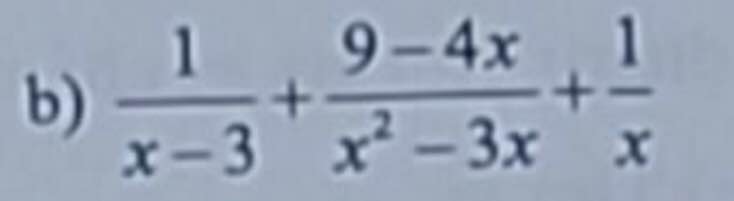
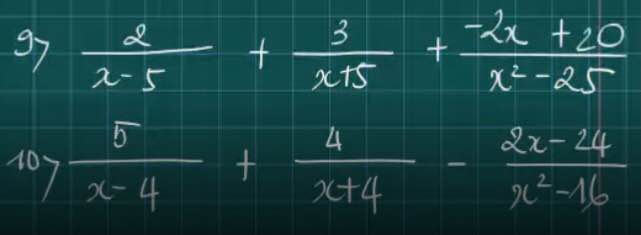
ĐKXĐ: \(x\notin\left\{0;-2;2\right\}\)
\(\dfrac{x+4}{x^2-4}-\dfrac{1}{x^2+2x}\)
\(=\dfrac{x+4}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x\left(x+2\right)}\)
\(=\dfrac{x\left(x+4\right)-x+2}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x^2+3x+2}{x\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{\left(x+2\right)\left(x+1\right)}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x+1}{x\left(x-2\right)}\)