
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

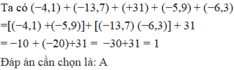

Bài 5 :
a, ( -4,8 ) + \(\left[\left(-5,7\right)+\left(4,8\right)\right]\)
= (-4,8) + ( 4,8 ) + ( -5,7 )
= (-5,7 )
b) [(-9,6) + (+1,5)] + [(+9,6) + (-1,5)]
= (-9,6 ) + 9,6 + 1,5 + ( -1,5 )
= 0
c) (3,1 - 2,5) - (-2,5 + 3,1)
= 3,1 - 2,5 + 2,5 - 3,1
= 3,1 -3,1 -2,5 + 2,5
=0
= 3,1 - 2,5 + 2,5 + 3,1
= ( 3,1 - 3,1 ) + ( -2,5 - 2,5 )
= 0
d) 2,7 - (-4,3) + (-8,5) - (-0,6)
= 2,7 + 4,3 - 7 ,9
= 7 - 7,9
= -0,9
d) 2,7 - (-4,3) + (-8,5) - (-0,6)
= 2,7 + 4,3 + 8,5 + 0,6
= 7 + 9,1
= 16,1
e, - \(\left(\dfrac{3}{5}+\dfrac{3}{4}\right)-\left(\dfrac{3}{4}+\dfrac{2}{5}\right)\)
= \(\dfrac{-3}{5}+\dfrac{3}{4}-\dfrac{3}{4}-\dfrac{2}{5}\)
= \(\dfrac{-3}{5}-\dfrac{2}{5}+\dfrac{3}{4}-\dfrac{3}{4}\)
= -1
f) [(-4,9) + (-37,8)] + [(+1,9) + (+2,8)]
= - 4,9 - 37,8 + 1,9 + 2,8
= ( -4,9 + 1,9 ) + ( -37,8 + 2,8 )
= -3 + (-35)
= -38
g) (-4,1) + (-13,7) + (+31) + (-5,9) + (-6,3)
= (-4,1) + ( -5,9 ) + ( -13,7 ) + ( -6,3) + 31
= - 10 - 20 + 31
= 1
h) (-6,5) . 2,8 + 2,8 . (-3,5)
= 2,8 . [ -6,5 - 3,5 ]
= 2,8 . (-10 )
= - 28

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
b+c+d/a=c+d+a/b=d+a+b/c=a+b+c/d=3(a+b+c+d)/a+b+c+d=3
suy ra k=3
taco:\(\dfrac{b+c+d}{a}=\dfrac{c+d+a}{b}+\dfrac{d+a+b}{c}=\dfrac{a+b+c}{d}=k\)=>\(\dfrac{b+c+d}{a}+1=\dfrac{c+d+a}{b}+1=\dfrac{a+b+d}{c}+1=\dfrac{a+b+c}{d}+1=k+1\)=>\(\dfrac{a+b+c+d}{a}=\dfrac{a+b+c+d}{b}=\dfrac{a+b+c+d}{c}=\dfrac{a+b+c+d}{d}=k+1=\dfrac{a+b+c+d+a+b+c+d+a+b+c+d}{a+b+c+d}=\dfrac{4.\left(a+b+c+d\right)}{a+b+c+d}=4\)
=>k+1=4
=>k=3

\(1)\)\(\frac{\overline{ab}}{b}=\frac{\overline{bc}}{c}=\frac{\overline{ca}}{a}\)
\(\Leftrightarrow\)\(\frac{10a+b}{b}=\frac{10b+c}{c}=\frac{10c+a}{a}\)
\(\Leftrightarrow\)\(\frac{10a}{b}=\frac{10b}{c}=\frac{10c}{a}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{10a}{b}=\frac{10b}{c}=\frac{10c}{a}=\frac{10a+10b+10c}{a+b+c}=\frac{10\left(a+b+c\right)}{a+b+c}=10\)
Do đó :
\(\frac{10a}{b}=10\)\(\Leftrightarrow\)\(a=b\)
\(\frac{10b}{c}=10\)\(\Leftrightarrow\)\(b=c\)
\(\frac{10c}{a}=10\)\(\Leftrightarrow\)\(c=a\)
\(\Rightarrow\)\(a=b=c\)
\(\Rightarrow\)\(A=\left(a-b\right)\left(b-c\right)\left(c-a\right)+2016=2016\)
\(2)\)\(\frac{\overline{ab}+\overline{bc}}{a+b}=\frac{\overline{bc}+\overline{ca}}{b+c}=\frac{\overline{ca}+\overline{ab}}{c+a}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{\overline{ab}+\overline{bc}}{a+b}=\frac{\overline{bc}+\overline{ca}}{b+c}=\frac{\overline{ca}+\overline{ab}}{c+a}=\frac{2\left(\overline{ab}+\overline{bc}+\overline{ca}\right)}{2\left(a+b+c\right)}=\frac{\overline{ab}+\overline{bc}+\overline{ca}}{a+b+c}\)
\(=\frac{10a+b+10b+c+10c+a}{a+b+c}=\frac{11a+11b+11c}{a+b+c}=\frac{11\left(a+b+c\right)}{a+b+c}=11\)
Do đó :
\(\frac{\overline{ab}+\overline{bc}}{a+b}=11\)\(\Leftrightarrow\)\(10a+11b+c=11a+11b\)\(\Leftrightarrow\)\(c=a\)
\(\frac{\overline{bc}+\overline{ca}}{b+c}=11\)\(\Leftrightarrow\)\(10b+11c+a=11b+11c\)\(\Leftrightarrow\)\(a=b\)
\(\frac{\overline{ca}+\overline{ab}}{c+a}=11\)\(\Leftrightarrow\)\(10c+11a+b=11c+11a\)\(\Leftrightarrow\)\(b=c\)
\(\Rightarrow\)\(a=b=c\)
\(\Rightarrow\)\(M=\left(\frac{b}{a}+1\right)\left(\frac{c}{b}+1\right)\left(\frac{a}{c}+1\right)+2016=2.2.2+2016=2024\)
Chúc bạn học tốt ~
Ta có: \(\frac{a}{b+c+d}=\frac{b}{a+c+d}=\frac{c}{a+b+d}=\frac{d}{a+b+c}\)
\(\Rightarrow\frac{a}{b+c+d}+1=\frac{b}{a+c+d}+1=\frac{c}{a+b+d}+1=\frac{d}{a+b+c}+1\)
hay \(\frac{a+b+c+d}{b+c+d}=\frac{a+b+c+d}{a+c+d}=\frac{a+b+c+d}{a+b+d}=\frac{a+b+c+d}{a+b+c}\)
Do các tử số trên bằng nhau nên các mẫu số cũng bằng nhau hay \(b+c+d=a+c+d=a+b+d=a+b+c\)
Suy ra a = b =c =d
\(\Rightarrow A=\frac{a+b}{c+d}+\frac{b+c}{a+d}+\frac{c+d}{a+b}+\frac{d+a}{b+c}=1+1+1+1=4\)

Ta có :\(\frac{a+b}{ab}=\frac{b+c}{bc}=\frac{c+a}{ca}\)
\(\Rightarrow\frac{1}{a}+\frac{1}{b}=\frac{1}{b}+\frac{1}{c}=\frac{1}{c}+\frac{1}{a}\)
\(\Rightarrow\frac{1}{a}=\frac{1}{c};\frac{1}{b}=\frac{1}{a};\frac{1}{c}=\frac{1}{b}\)
\(\Rightarrow\frac{1}{a}=\frac{1}{b}=\frac{1}{c}\)
\(\Rightarrow a=b=c\)
\(\Rightarrow ab=bc=ca=a^2=b^2=c^2\)
\(\Rightarrow ab+bc+ca=a^2+b^2+c^2\)
\(\Rightarrow\frac{ab+bc+ca}{a^2+b^2+c^2}=1\)
Vậy M=1

Bài 1 :
a) x < 0
b) x > 0
c) <=> 3 + |3x - 1| = 5
<=> |3x - 1| = 5 - 3 = 2
<=> 3x - 1 = 2 hoặc -3x + 1 = 2
<=> 3 x = 3 hoặc -3x = 1
<=> x = 1 hoặc x = -1/3
Bài 2 :
a) 27 = 33 < 3n < 243 = 35
<=> 3 < n < 5
Vì n thuộc N* nên n thuộc {4; 5}
b) 32 = 25 < 2n < 128 = 27
<=> 5 < n < 7. Vì n thuộc N* nên n = 6
c) 125 = 5 . 25 = 5 . 52 < 5.5n < 5 . 125 = 5 . 53
<=> 2 < n < 3. Vì n thuộc N* nên n = 3

Lời giải:
\(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk, c=dk \)
Khi đó:
\(\frac{2002a+2003b}{2002a-2003b}=\frac{2002bk+2003b}{2002bk-2003b}=\frac{b(2002k+2003)}{b(2002k-2003)}=\frac{2002k+2003}{2002k-2003}(1)\)
\(\frac{2002c+2003d}{2002c-2003d}=\frac{2002dk+2002d}{2002dk-2003d}=\frac{d(2002k+2003)}{d(2002k-2003)}=\frac{2002k+2003}{2002k-2003}(2)\)
Từ \((1);(2)\Rightarrow \frac{2002a+2003b}{2002a-2003b}=\frac{2002c+2003d}{2002c-2003d}\)
Ta có đpcm.
Xét tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) . Gọi giá trị chung của các tỉ số đó là k, ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=> \(a=k.b,c=k.d\)
Ta có :
( 1 )
= \(\dfrac{2002a+2003b}{2002a-2003b}=\dfrac{2002kb+2003b}{2002kb-2003b}\)
= \(\dfrac{b.\left(2002k+2003\right)}{b.\left(2002k-2003\right)}=\dfrac{2002k+2003}{2002k-2003}\)
( 2 ) \(\dfrac{2002c+2003d}{2002c-2003d}=\dfrac{2002kd+2003d}{2002kd-2003d}\)
= \(\dfrac{d.\left(2002k+2003\right)}{d.\left(2002k-2003\right)}=\dfrac{2002k+2003}{2002k-2003}\)
Từ ( 1 ) và ( 2 ) => \(\dfrac{2002a+2003b}{2002a-2003b}=\dfrac{2002c+2003d}{2002c-2003d}\)

a: 3,26-1,549=1,711
b: 0,167-2,396=-2,229
c: -3,29-0,867=-4,157
d: -6,09-3,65=-9,74
e: \(\left(-2.5\right)\cdot\left(-4\right)=2.5\cdot4=10\)
f: \(=\left[\left(-2.5\right)\cdot\left(-4\right)\right]\cdot\left(-7\right)=-7\cdot10=-70\)

a: 3,26-1,549=1,711
b: 0,167-2,396=-2,229
c: -3,29-0,867=-4,157
d: -6,09-3,65=-9,74
e: \(\left(-2.5\right)\cdot\left(-4\right)=2.5\cdot4=10\)
f: \(=\left[\left(-2.5\right)\cdot\left(-4\right)\right]\cdot\left(-7\right)=-7\cdot10=-70\)