Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

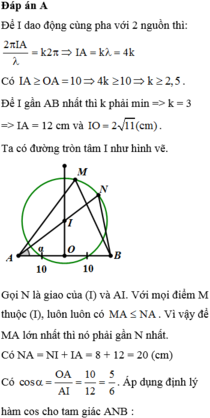
B N 2 = A N 2 + A B 2 - 2 A N . A B . cos α = 400 3 ⇒ B N = 20 3 c m


Đáp án C
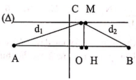
Điểm M dao động với biên độ cực tiểu khi: 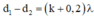
Điểm M gần C nhất khi k-1: ![]()
Gọi CM=OH=x, khi đó:
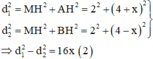
Từ (1) và (2) ta có: ![]()
Từ (1) và (3) ta có: ![]()
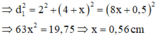

Đáp án A
+ Giả sử M và P thuộc các đường cực đại thì khi đó M A − M B = k λ = 7 , 5 c m và P A − P B = k + 2 λ = 13 , 5 c m . Suy ra λ = 3 c m .
Tuy nhiên khi đó k = 2 , 5 không phải là số nguyên nên trường hợp này loại
+ Giả sử M và P thuộc các đường cực tiểu thì khi đó M A − M B = k + 1 / 2 λ = 7 , 5 c m và P A − P B = k + 1 / 2 + 2 λ = 13 , 5 c m . Suy ra λ = 3 c m . Khi kiểm tra lại thấy k = 2 thỏa mãn
+ M' đối xứng với M qua trung điểm của AB suy ra M ' A − M ' B = − 7 , 5 c m
- Số điểm dao động với biên độ cực đại trên M M ' là:
M ' A − M ' B ≤ k λ ≤ M A − M B ⇔ − 7 , 5 ≤ k .3 ≤ 7 , 5 ⇔ − 2 , 5 ≤ k ≤ 2 , 5.
Vậy có 5 điểm dao động với biên độ cực đại trên M M ' .
- Số điểm dao động với biên độ cực tiểu trên M M ' là:
M ' A − M ' B ≤ k + 0 , 5 λ ≤ M A − M B ⇔ − 7 , 5 ≤ k + 0 , 5 .3 ≤ 7 , 5 ⇔ − 3 ≤ k ≤ 2.
Vậy có 6 điểm dao động với biên độ cực tiểu trên M M '
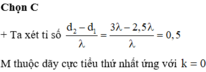
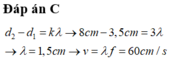
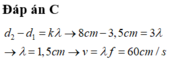
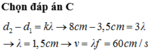

Đáp án C
+ Xét tỉ số M A - M B λ = 6 4 = 1 , 5 -> M thuộc cực tiểu thứ 2 tính từ trung trực AB.