Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

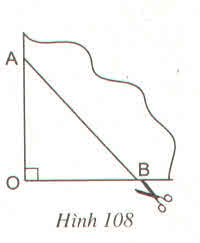
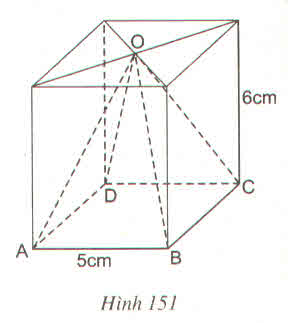
Tứ giác nhận được theo nhát cắt AB là hình thoi vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau. Nếu có thêm OA = OB thì hình thoi nhận được có hai đường chéo bằng nhau nên là hình vuông.

Hình 58:
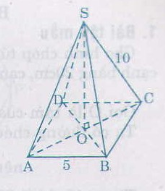
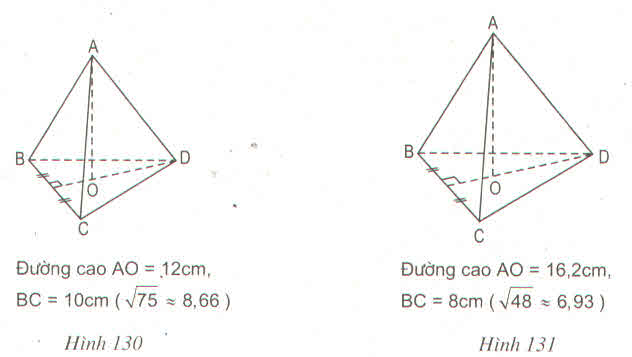
Đáy của hình chóp là tam giác đều cạnh bằng 10cm
Đường cao của tam giác đều là:
HD = √DC2−HC2DC2−HC2 = √102−52102−52 = √75 ≈ 8,66 (cm)
Diện tích đáy của hình chóp đều là:
S = 1212.BC.h = 1212. 10. 8,66 = 43,3(cm2)
Thể tích hình chóp đều là:
V =1313. S. h1 = 1313. 43,3 .12 = 173,2(cm3)
Hình 59:
Đường cao của tam giác đều BDC:
h = √DC2−(BC2)2DC2−(BC2)2
= √82−4282−42 = √48 ≈6,93(cm)
Diện tích đáy của hình chóp đều là:
S = 1212.BC.h = 1212.8.6,93 = 27,72(cm2)
Thể tích hình chóp đều là:
V = 1313. S. h1 = 1313. 27,72. 16,2 =149,69(cm3)

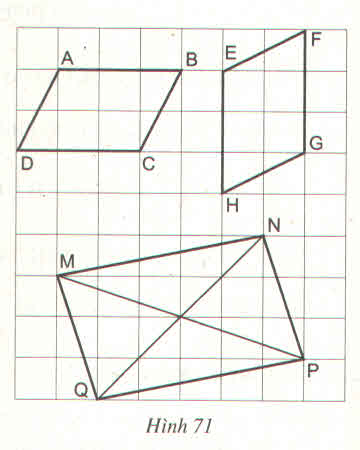
Cả ba tứ giác là hình bình hành.
- Tứ giác ABCD là hình bình hành vì có
AB // CD và AB = CD =3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có
EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = QP và MQ = NP (dấu hiệu nhận biết 2)

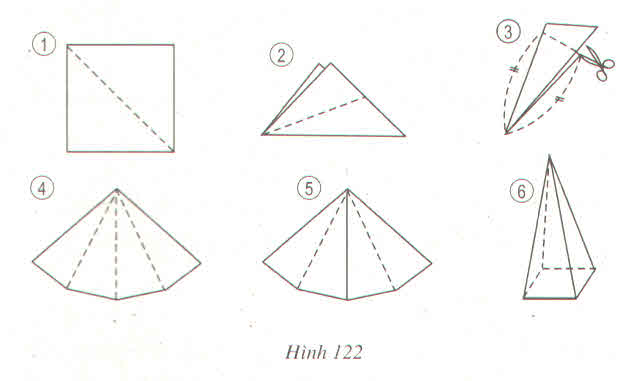
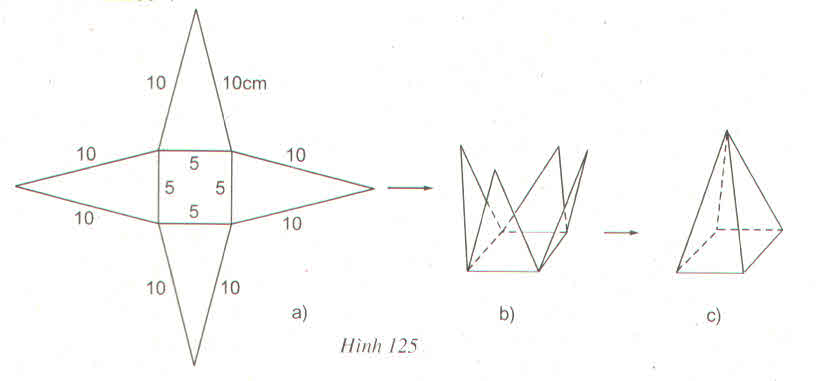
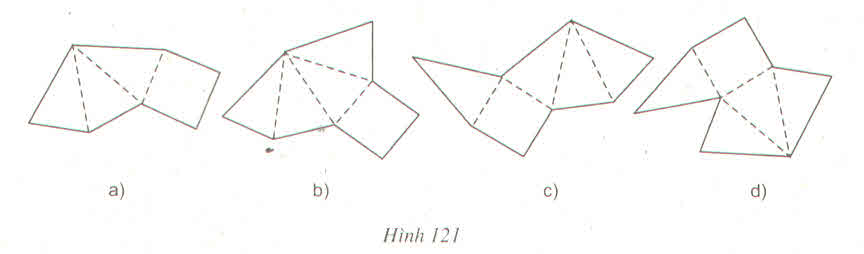
Hình a, khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d, khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.