Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\sqrt{\sqrt{2\sqrt{6}+6+2\sqrt{2}+2\sqrt{3}-\sqrt{5+2\sqrt{6}}}}\)
\(=\sqrt{1+\sqrt{2}+\sqrt{3}-\left(\sqrt{3}+\sqrt{2}\right)}=1\)
b) \(A=\sqrt{x^2-6x+9}-\dfrac{x^2-9}{\sqrt{9-6x+x^2}}\)
\(=\left|x-3\right|-\dfrac{\left(x-3\right)\left(x+3\right)}{\left|x-3\right|}\)
Th1: x-3 < 0
\(A=\left(3-x\right)-\dfrac{\left(x-3\right)\left(x+3\right)}{3-x}=3-x+x-3=0\)
Th2: x-3 > 0
\(A=x-3-\dfrac{\left(x-3\right)\left(x+3\right)}{x-3}=x-3-\left(x+3\right)=-6\)
c)
Đk: x >/ 1 \(B=\dfrac{\sqrt{x+\sqrt{4\left(x-1\right)}}-\sqrt{x-\sqrt{4\left(x-1\right)}}}{\sqrt{x^2-4\left(x-1\right)}}\cdot\left(\sqrt{x-1}-\dfrac{1}{\sqrt{x-1}}\right)\)
\(=\dfrac{\sqrt{x+2\sqrt{x-1}}-\sqrt{x-2\sqrt{x-1}}}{\sqrt{x^2-4\left(x-1\right)}}\cdot\dfrac{x-2}{\sqrt{x-1}}\)
\(=\dfrac{\sqrt{x-1}+1-\left|\sqrt{x-1}-1\right|}{\left|x-2\right|}\cdot\dfrac{x-2}{\sqrt{x-1}}\)
Th1: \(x-2\ge0\Leftrightarrow x\ge2\)
\(B=\dfrac{\sqrt{x-1}+1-\sqrt{x-1}+1}{x-2}\cdot\dfrac{x-2}{\sqrt{x-1}}=\dfrac{2}{\sqrt{x-1}}\)
Th2: \(x-2\le0\Leftrightarrow x\le2\)
kết hợp với đk, ta được: 1 \< x \< 2
\(=\dfrac{\sqrt{x-1}+1-\sqrt{x-1}-1}{2-x}\cdot\dfrac{x-2}{\sqrt{x-1}}=0\)
d) \(A=\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}=\sqrt{x-2}+\sqrt{2}+\left|\sqrt{x-2}-\sqrt{2}\right|=\sqrt{x-2}+\sqrt{2}-\sqrt{x-2}+\sqrt{2}=2\sqrt{2}\)
chẳng biết có sai sót gì 0 nữa, xin lỗi tớ 0 xem lại đâu vì chán quá!

1. b) \(\left(x\sqrt{\dfrac{6}{x}}+\sqrt{\dfrac{2x}{3}}+\sqrt{6x}\right):\sqrt{6x}\)
=\(\left(x\sqrt{\dfrac{6x}{x^2}}+\sqrt{\dfrac{6x}{9}}+\sqrt{6x}\right):\sqrt{6x}\)
=\(\left(\sqrt{6x}+\dfrac{1}{3}\sqrt{6x}+\sqrt{6x}\right):\sqrt{6x}\)
=\(\dfrac{7}{3}\sqrt{6x}:\sqrt{6x}=\dfrac{7}{3}\)
2.
P=\(\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)(bn có ghi sai đề ko)
a) ĐKXĐ : \(x\ge1,x\ge2,x\ge0\)
b) P=\(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}+\dfrac{x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
=\(\dfrac{x-3\sqrt{x}-\sqrt{x}+3-2x+\sqrt{x}+4\sqrt{x}-2+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
=\(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}=\dfrac{1}{\sqrt{x}-2}\)
c) thay x= \(4-2\sqrt{3}\)vào P ta có :
\(\dfrac{1}{\sqrt{4-2\sqrt{3}}-2}=\dfrac{1}{\sqrt{3}-1-2}=\dfrac{1}{\sqrt{3}-3}\)

a: \(A=\dfrac{-\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}+3}-\dfrac{\left(\sqrt{x}-3\right)^2}{\sqrt{x}-3}-6\)
\(=-\sqrt{x}+3-\sqrt{x}+3-6=-2\sqrt{x}\)
b: \(\left(\dfrac{2\sqrt{x}}{x\sqrt{x}+x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right):\left(\dfrac{2\sqrt{x}}{\sqrt{x}+1}-1\right)\)
\(=\left(\dfrac{2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(x+1\right)}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{2\sqrt{x}-\sqrt{x}-1}{\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}-x-1}{\left(\sqrt{x}+1\right)\left(x+1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{1}{x+1}\)
g: \(\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right)\left(\dfrac{x-1}{\sqrt{x}+1}-2\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1}{x-1}\cdot\left(\sqrt{x}-1-2\right)\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{x-1}\)

\(a.R=\left(\dfrac{\sqrt{x}+1}{\sqrt{xy}+1}+\dfrac{\sqrt{x}\left(\sqrt{y}+1\right)}{1-\sqrt{xy}}+1\right):\left(1-\dfrac{\sqrt{x}+1}{\sqrt{xy}+1}-\dfrac{\sqrt{x}\left(\sqrt{y}+1\right)}{\sqrt{xy}-1}\right)\)
\(R=\left[\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{xy}-1\right)-\sqrt{x}\left(\sqrt{y}+1\right)\left(\sqrt{xy}+1\right)+xy-1}{\left(\sqrt{xy}+1\right)\left(\sqrt{xy}-1\right)}\right]:\left[\dfrac{xy-1-\left(\sqrt{x}+1\right)\left(\sqrt{xy}-1\right)-\sqrt{x}\left(\sqrt{y}+1\right)\left(\sqrt{xy}+1\right)}{\left(\sqrt{xy}+1\right)\left(\sqrt{xy}-1\right)}\right]\)
\(R=\dfrac{x\sqrt{y}-\sqrt{x}+\sqrt{xy}-1-xy-\sqrt{xy}-x\sqrt{y}-\sqrt{x}+xy-1}{xy-1}:\dfrac{xy-1-x\sqrt{y}+\sqrt{x}+\sqrt{xy}+1-xy-\sqrt{xy}-x\sqrt{y}-\sqrt{x}}{xy-1}\)
\(R=\dfrac{-2\sqrt{x}-2}{xy-1}:\dfrac{-2x\sqrt{y}-2\sqrt{xy}}{xy-1}\)
\(R=\dfrac{-2\left(\sqrt{x}+1\right)}{xy-1}.\dfrac{xy-1}{-2\left(x\sqrt{y}+\sqrt{xy}\right)}\)
\(R=\dfrac{\sqrt{x}+1}{x\sqrt{y}+\sqrt{xy}}\)
\(b.C=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{7\sqrt{x}+4}{x-\sqrt{x}-6}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
\(C=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}+\dfrac{7\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}\)
\(C=\dfrac{2x-6\sqrt{x}+7\sqrt{x}+4-x-4\sqrt{x}-4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}\)
\(C=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)}\)
\(C=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(c.M=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{\sqrt{x}+x}=\dfrac{\sqrt{x}+1+x}{x+\sqrt{x}}.\dfrac{\sqrt{x}+x}{\sqrt{x}}=\dfrac{\sqrt{x}+1+x}{\sqrt{x}}\)

Mình làm mấy bài rút gọn thôi nhé :v (mấy cái kia mình làm sợ không đúng)
\(P=\dfrac{\sqrt{x}+1}{x-1}-\dfrac{x+2}{x\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\\ =\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\\ =\dfrac{1}{\sqrt{x}-1}-\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}\)
\(=\dfrac{x+\sqrt{x}+1-\left(x+2\right)-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{x+\sqrt{x}+1-x-2-\left(x-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}+1-2-x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}+0-x}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(1-\sqrt{x}\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left[-\left(\sqrt{x}-1\right)\right]}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(-1\right)}{x+\sqrt{x}+1}\\ =-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
Bài 3:
\(P=\dfrac{x-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\\ =\dfrac{x-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{\left(2x+\sqrt{x}\right)\sqrt{x}}{x}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\\ =\dfrac{x-\sqrt{x}}{x+\sqrt{x}+1}+2\left(\sqrt{x}+1\right)\\ =\dfrac{x-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{x\left(2\sqrt{x}+1\right)}{x}+2\sqrt{x}+2\)
\(=\dfrac{x-\sqrt{x}}{x+\sqrt{x}+1}-\left(2\sqrt{x}+1\right)+2\sqrt{x}+2\\ =\dfrac{x-\sqrt{x}}{x+\sqrt{x}+1}-2\sqrt{x}-1+2\sqrt{x}+2\\ =\dfrac{x-\sqrt{x}}{x+\sqrt{x}+1}+1\\ =\dfrac{x-\sqrt{x}+x+\sqrt{x}+1}{x+\sqrt{x}+1}\\ =\dfrac{2x+1}{x+\sqrt{x}+1}\)

a: \(VT=\dfrac{3\sqrt{6}}{2}+\dfrac{2\sqrt{6}}{3}-\dfrac{4\sqrt{6}}{2}\)
\(=\dfrac{-\sqrt{6}}{2}+\dfrac{2\sqrt{6}}{3}=\dfrac{-3\sqrt{6}+4\sqrt{6}}{6}=\dfrac{\sqrt{6}}{6}\)
b: \(VT=\dfrac{\left(\sqrt{6x}+\dfrac{\sqrt{6x}}{3}+\sqrt{6x}\right)}{\sqrt{6x}}\)
\(=1+\dfrac{1}{3}+1=2\dfrac{1}{3}\)

\(A=\sqrt{\dfrac{18-3\sqrt{3}}{11}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{\sqrt{11\left(18-3\sqrt{3}\right)}}{11}-\dfrac{\sqrt{4+2\sqrt{3}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{11\left(18-3\sqrt{3}\right)}}{11}-\dfrac{\sqrt{3}+1}{\sqrt{2}}\)
\(=\dfrac{\sqrt{11\left(18-3\sqrt{3}\right)}}{11}-\dfrac{\sqrt{6}+\sqrt{2}}{2}\)
\(=\dfrac{2\sqrt{11\left(18-3\sqrt{3}\right)}-11\sqrt{6}-11\sqrt{2}}{22}\)
b: \(=\dfrac{x\sqrt{x}-2x+28-x+16-x-9\sqrt{x}-8}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x\sqrt{x}-4x-9\sqrt{x}+36}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}=\dfrac{x-9}{\sqrt{x}+1}\)

a: \(=\dfrac{2\sqrt{7}-10-6+\sqrt{7}}{4}+\dfrac{24+6\sqrt{7}-20+5\sqrt{7}}{9}\)
\(=\dfrac{3\sqrt{7}-16}{4}+\dfrac{4+11\sqrt{7}}{9}\)
\(=\dfrac{27\sqrt{7}-144+16+44\sqrt{7}}{36}=\dfrac{71\sqrt{7}-128}{36}\)
b: \(=\dfrac{\sqrt{y}\left(x+y\right)}{\sqrt{xy}}\cdot\dfrac{\sqrt{x}-\sqrt{y}}{x+y}\)
\(=\dfrac{\sqrt{x}-\sqrt{y}}{\sqrt{x}}\)
c: \(=\left(\dfrac{\left(\sqrt{x}-1\right)\left(3\sqrt{x}+1\right)+3\sqrt{x}-1}{\left(3\sqrt{x}-1\right)\left(3\sqrt{x}+1\right)}\right)\cdot\dfrac{3\sqrt{x}-1}{3\sqrt{x}-5}\)
\(=\dfrac{3x+\sqrt{x}-3\sqrt{x}-1+3\sqrt{x}-1}{3\sqrt{x}+1}\cdot\dfrac{1}{3\sqrt{x}-5}\)
\(=\dfrac{3x+\sqrt{x}-2}{\left(3\sqrt{x}+1\right)}\cdot\dfrac{1}{3\sqrt{x}-5}\)
\(=\dfrac{3x+\sqrt{x}-2}{\left(3\sqrt{x}+1\right)\left(3\sqrt{x}-5\right)}\)
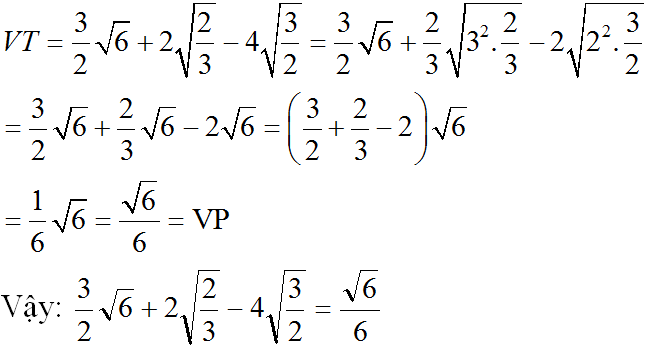
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne4\end{matrix}\right.\)
\(\left(\dfrac{6x+4\sqrt{x}}{x\sqrt{x}-4\sqrt{x}}-\dfrac{6}{3\sqrt{x}+6}+1\right):\dfrac{1}{\sqrt{x}-2}\)
\(=\left(\dfrac{2\sqrt{x}\left(3\sqrt{x}+2\right)}{\sqrt{x}\left(x-4\right)}-\dfrac{6}{3\left(\sqrt{x}+2\right)}+1\right):\dfrac{1}{\sqrt{x}-2}\)
\(=\left(\dfrac{2\left(3\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{2}{\sqrt{x}+2}+1\right):\dfrac{1}{\sqrt{x}-2}\)
\(=\dfrac{6\sqrt{x}+4-2\left(\sqrt{x}-2\right)+x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{1}\)
\(=\dfrac{x+6\sqrt{x}-2\sqrt{x}+4}{\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}+2\right)}\)
\(=\sqrt{x}+2\)