Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Số cách chọn một người trong đoàn là: 31.
Số người đến từ Hà Nội hoặc đến từ Hải Phòng là: 7 + 5 = 12.
Vậy xác suất để người đó đến từ Hà Nội hoặc đến từ Hải Phòng là \(\dfrac{12}{31}\).
Số cách chọn người đến từ Hà Nội hoặc đến từ Hải Phòng là:
7+5=12(cách)
Xác suất chọn người đến từ Hà Nội hoặc đến từ Hải Phòng là:
P=12/31
Đáp án : B
Với mỗi bóng đèn ta có hai sự lựa chọn trạng thái là bật hoặc tắt. Như vậy, theo quy tắc nhân sẽ có cách lựa chọn bật, tắt các bóng đèn đó.
Tuy nhiên có một trạng thái duy nhất là khi cả 10 bóng đèn đều tắt thì phòng không có ánh sáng. Vậy để phòng có ánh sáng thì có cách bật, tắt các bóng đèn.
Đáp án B
Có n ( Ω ) = C 12 3
Giả sử chọn 3 người có số thứ tự trong hàng lần lượt là a, b, c
Theo giả thiết ta có: a < b < c, b – a > 1, c – b > 1, a , b , c ∈ { 1 , 2 , . . . , 12 } .
, gọi 
là tập các số tự nhiên khác nhau có 
chữ số khác nhau được lập từ các số của tập 
. Chọn ngẫu nhiên một số trong tập
Đáp án A
Số cách đi ra của 8 người bằng 13 8
Số cách đi ra của 8 người mà mỗi người một tầng bằng A 13 8
Xác suất cần tính bằng
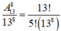
1. Không gian mẫu: \(C_{30}^2\)
Trong 3 số nguyên dương đầu tiên có 15 số chẵn và 15 số lẻ
Hai số có tổng là chẵn khi chúng cùng chẵn hoặc lẻ
\(\Rightarrow C_{15}^2+C_{15}^2\) cách lấy 2 số có tổng chẵn
Xác suất: \(P=\dfrac{C_{15}^2+C_{15}^2}{C_{30}^2}=...\)
2. ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow tan3x=cot\left(\dfrac{\pi}{2}-x\right)\)
\(\Leftrightarrow tan3x=tanx\)
\(\Rightarrow3x=x+k\pi\)
\(\Rightarrow x=\dfrac{k\pi}{2}\)
\(\Rightarrow x=k\pi\)
Có 2 điểm biểu diễn
Chọn C
Ta có: 
Gọi A là biến cố “trong 3 người được chọn đó không có 2 người ngồi kề nhau”
=> A ¯ là biến cố “trong 3 người đươc chọn có ít nhất 2 người ngồi kề nhau”
TH 1: 3 người ngồi kề nhau có 13 cách chọn.
TH 2: có 2 người ngồi cạnh nhau
- Hai người ngồi cạnh nhau ngồi đầu hàng có 2 cách chọn, với mỗi cách chọn như vậy có 12 cách chọn người còn lại vậy có: 2.12=24 cách.
- Hai người ngồi cạnh nhau không ngồi đầu hàng có 12 cách chọn, với mỗi cách chọn như vậy có 11 cách chọn người còn lại vậy có: 11.12=132 cách.
