Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
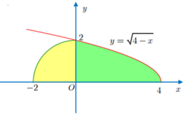
Ta có V = π ∫ 0 π − sin x 2 d x = π ∫ 0 π sin 2 x d x

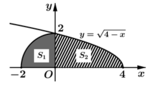
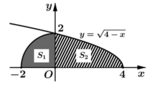
Phương trình hoành độ giao điểm: ![]()
• Thể tích vật thể khi quay phần S 1 quanh trục hoành là nửa khối cầu bán kính R = 2 nên có thể tích bằng
![]()
• Thể tích vật thể khi quay phần S 2 quanh trục hoành là
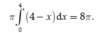
Vậy thể tích cần tính ![]()
Chọn A.

Đáp án C
Thể tích khối tròn xoay cần tính là V H = π . ∫ 1 k lnx d x ⇒ I = ∫ 1 k lnx d x .
Đặt u = ln x d v = d x ⇔ d u = d x x v = x suy ra I = x . ln x 1 k - ∫ 1 k d x = x . ln x - 1 1 k = k . ln k - 1 + 1 .
Mặt khác V H = π . I = π ⇒ I = 1 suy ra k . ln k - 1 + 1 = 1 ⇔ k . ln k - 1 = 0 ⇔ k = e .
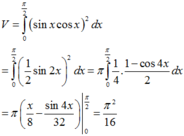
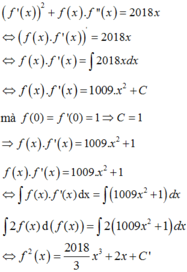
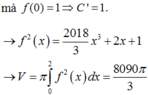
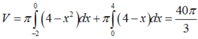

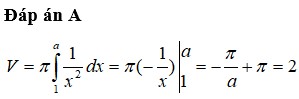
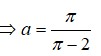
Đáp án D.
Ta có
x 2 + y − a 2 = R 2 ⇔ y = a ± R 2 − x 2
Nửa trên hình tròn có phương trình là y = a + R 2 − x 2
Nửa dưới hình tròn có phương trình là y = a − R 2 − x 2
Thể tích của hình xuyến là
V = V 1 − V 2 = π ∫ − R R a + R 2 − x 2 2 d x − π ∫ − R R a − R 2 − x 2 2 d x = 4 π a ∫ − R R R 2 − x 2 d x
Đặt x = R sin t ⇒ d x = R costdt x = − R ⇒ t = − π 2 ; x = R = t = π 2
⇒ V = 4 π a ∫ − π 2 π 2 R 2 − R 2 sin 2 t . R cos t d t = 4 π a R 2 ∫ − π 2 π 2 cos 2 t d t = 2 π 2 a R 2