Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
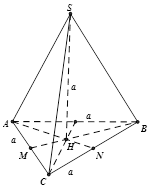
$H$ là chân đường cao của hình chóp đều nên $H$ chính là tâm đường tròn ngoại tiếp tam giác $ABC$
Kẻ $HM\perp BC$. Dễ thấy $M$ là trung điểm $BC$ và $SBC$ cân tại $S$ nên $SM\perp BC$
Do đó:
$\angle ((SBC), (ABC))=\angle (SM, HM)$
$=\widehat{SMH}=60^0$
$\frac{SH}{HM}=\tan \widehat{SMH}=\tan 60^0=\sqrt{3}$
$\Rightarrow SH=\sqrt{3}HM$
Mà: $HM=\frac{1}{3}AM=\frac{1}{3}.\sqrt{AB^2-BM^2}=\frac{1}{3}\sqrt{AB^2-(\frac{BC}{2})^2}=\frac{\sqrt{3}}{6}a$
Do đó: $SH=\sqrt{3}HM=\frac{3}{6}a=\frac{1}{2}a$

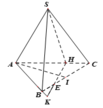
Trong mp (SAB), qua B dựng đường thẳng song song SH, cắt tia AS kéo dài tại D
\(\Rightarrow\) SH là đường trung bình tam giác ABD \(\Rightarrow BD=2SH\) và \(BD\perp\left(ABC\right)\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow AC\perp\left(BDM\right)\)
Trong mp (BDM), kẻ \(BK\perp DM\Rightarrow BK\perp\left(SAC\right)\Rightarrow\widehat{BSK}\) là góc giữa SB và (SAC)
\(\Rightarrow\widehat{BSK}=45^0\Rightarrow SB=BK\sqrt{2}\)
\(\Rightarrow AD=2SA=2SB=2\sqrt{2}BK\Rightarrow BD^2=AD^2-AB^2=8BK^2-4a^2\) (1)
Mặt khác: \(\dfrac{1}{BK^2}=\dfrac{1}{BM^2}+\dfrac{1}{BD^2}\Rightarrow\dfrac{1}{BK^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\) (2)
(1);(2) \(\Rightarrow\left\{{}\begin{matrix}BD^2=8BK^2-4a^2\\\dfrac{1}{BK^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\end{matrix}\right.\)
\(\Rightarrow\dfrac{8}{BD^2+4a^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\Rightarrow BD\Rightarrow SH\)
Sao kết quả xấu vậy nhỉ?

\(+\) vì \(SH\perp\left(ABC\right)\) và \(AN\subset\left(ABC\right)\Rightarrow SH\perp AN\) hay \(\Rightarrow SH\perp AH\)
\(\Rightarrow\) \(AH\) là hình chiếu vuông góc của \(SA\) lên \(\left(ABC\right)\) \(\Rightarrow\left(SA,\left(ABC\right)\right)=\left(SA,AH\right)=\widehat{SAH}\)
\(+\) gọi \(M,N\) lần lượt là t/điểm \(AC,BC\)
vì \(\Delta ABC\) là tam giác đều cạnh \(a\) nên dễ tính được : \(AN=\dfrac{a\sqrt{3}}{2}\)
từ giả thiết , suy ra \(H\) là trọng tâm \(\Delta ABC\)
\(\Rightarrow\) \(AH=\dfrac{2}{3}AN=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
\(+\) áp dụng hệ thức lược trong tam giác \(SHA\) vuông tại \(H\) , có :
\(tan\widehat{SAH}\) \(=\dfrac{SH}{AH}=\dfrac{a}{\dfrac{a\sqrt{3}}{3}}=\sqrt{3}\Rightarrow\widehat{SAH}\) \(=60^o\)

a: \(SA=\sqrt{\left(\dfrac{a}{2}\right)^2\cdot2}=\sqrt{2}\cdot\dfrac{a}{\sqrt{2}}=a\)
\(SB=SA=a\)
AH=a/2; AD=a; góc A=120 độ
=>\(cosA=\dfrac{\dfrac{1}{4}a^2+a^2-DH^2}{2\cdot\dfrac{1}{2}a\cdot a}\)
=>\(\dfrac{5}{4}a^2-HD^2=a^2\cdot\dfrac{-1}{2}=\dfrac{-1}{2}a^2\)
=>HD^2=7/4a^2
=>\(HD=\dfrac{a\sqrt{7}}{2}\)
\(SD=\sqrt{SH^2+HD^2}=\sqrt{\dfrac{7}{4}a^2+\dfrac{1}{4}a^2}=a\sqrt{2}\)
Vì SA^2+AD^2=SD^2 và AS=AD
nên ΔASD vuôg cân tại A
(SD;BC)=(DS;DA)=góc SDA=45 độ

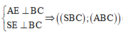
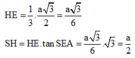

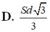

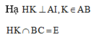
Đáp án A