Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC⊥CB
hay OE//AC
Xét ΔOBE vuông tại B có BH là đường cao
nên \(OH\cdot OE=OB^2=R^2\)
2: Xét ΔOBE và ΔOCE có
OB=OC
\(\widehat{BOE}=\widehat{COE}\)
OE chung
Do đó: ΔOBE=ΔOCE
Suy ra: \(\widehat{OBE}=\widehat{OCE}=90^0\)
hay EC là tiếp tuyến của (O)

1: ĐKXĐ: (x-3)(x+1)>=0
=>x>=3 hoặc x<=-1
2: ĐKXĐ: x(x+2)>=0
=>x>=0 hoặc x<=-2
3: ĐKXĐ: (x-4)(x+4)>=0
=>x>=4 hoặc x<=-4
4: DKXĐ: (x-2)(x+2)>=0
=>x>=2 hoặc x<=-2
6: ĐKXĐ: (x-6)(x+6)>=0
=>x>=6 hoặc x<=-6
7: ĐKXĐ: 2x-16>=0
=>x>=8
8: ĐKXĐ: x(x-1)>=0
=>x>=1 hoặc x<=0

\(\Leftrightarrow4.25^x-4.5^x+1=4y^4+8y^3+12y^2+16y+41\)
\(\Leftrightarrow\left(2.5^x-1\right)^2=4y^4+8y^3+12y^2+16y+41\)
Ta có:
\(4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+2\right)^2+8y+37>\left(2y^2+2y+2\right)^2\)
\(4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+5\right)^2+4\left(y-1\right)\left(3y+4\right)\ge\left(2y^2+2y+5\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+3\right)^2\\4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+4\right)^2\\4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+5\right)^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y^2-y-8=0\left(\text{không có nghiệm nguyên}\right)\\8y^2-25=0\left(\text{không có nghiệm nguyên}\right)\\\left(y-1\right)\left(3y+4\right)=0\end{matrix}\right.\)
\(\Rightarrow y=1\)
Thế vào pt ban đầu: \(25^x-5^x=20\)
Đặt \(5^x=t>0\Rightarrow t^2-t-20=0\Rightarrow\left[{}\begin{matrix}t=5\\t=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow5^x=5\Rightarrow x=1\)

Nhận xét: với mọi n nguyên thì \(n^2\equiv\left\{0;1;2;4\right\}\left(mod7\right)\)
Giả sử a;b tồn tại 1 số không chia hết cho 7
\(\Rightarrow a^2+b^2\equiv\left\{1;2;3;4;5;6;8\right\}\left(mod7\right)\)
\(\Rightarrow a^2+b^2\) luôn ko chia hết cho 7 (trái với giả thiết)
Vậy điều giả sử là sai hay \(a;b\) đều chia hết cho 7

Với p = 2 => 8p2 +1 = 33 (loại)
Với p = 3 => 8p2 + 1 = 73 (tm)
Với p > 3 => Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Với p = 3k + 1 => 8p2 + 1 = 8(3k + 1)2 + 1
= 72k2 + 48k + 9 = 3(24k2 + 16k + 3) \(⋮3\)(loại)
Với p = 3k + 2 => 8p2 + 1 = 8(3k + 2)2 + 1
= 72k2 + 96k + 33 = 3(24k2 + 32k + 11) \(⋮3\)(loại)
Vậy p = 3 thì 8p2 + 1 \(\in P\)
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\Rightarrow8p^2+1=73\) là số nguyên tố (thỏa mãn)
- Với \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(\Rightarrow p^2=3k+1\)
\(\Rightarrow8p^2+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) là số lớn hơn 3 và chia hết cho 3
\(\Rightarrow8p^2+1\) là hợp số (ktm)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu

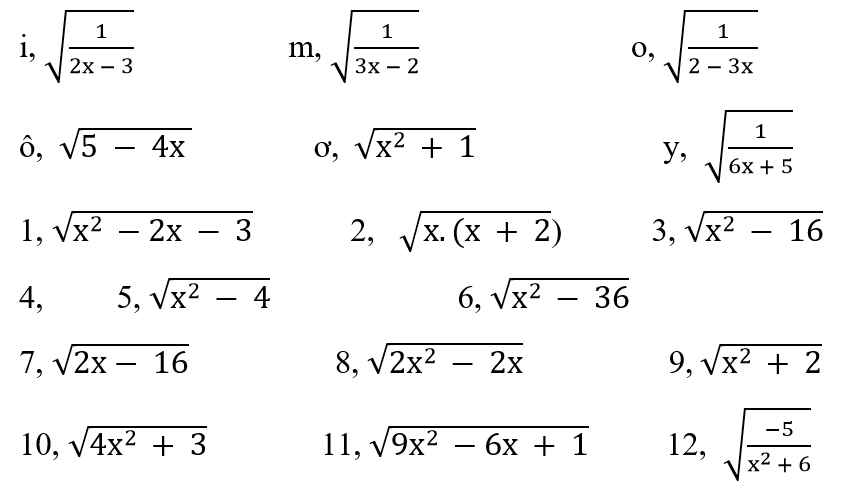
Dạng tổng quát: \(ax^2+bx+c\) hoặc \(ax+b\sqrt{x}+c\)
Khi đó em tìm: \(a.c=?\)
Ví dụ: \(-3x+10\sqrt{x}-7\) có \(a.c=\left(-3\right).\left(-7\right)=21\)
Sau đó em phân tích số đấy ra thành tích 2 số: \(21=\left(-3\right).\left(-7\right)=3.7\)
Và tổng của 2 số nào bằng \(b\) thì em tách \(bx\) thành 2 số đó (nhớ kèm ẩn x)
\(21=3.7\) và \(b=3+7=10\) nên ta tách thành: \(-3x+3\sqrt{x}+7\sqrt{x}-7\)
Lúc này đặt nhân tử chung thôi!
\(-3\sqrt{x}\left(\sqrt{x}-1\right)+7\left(\sqrt{x}-1\right)=\left(\sqrt{x}-1\right)\left(7-3\sqrt{x}\right)\)