TG
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
23 tháng 6 2018
Đáp án D
Ý tưởng bài toán: Với bài toán dạng này, ta thường chọn hai giá trị a, b bất kì, tính tổng f ( a ) + f ( b ) và tìm mối quan hệ giữa hai giá trị a, b.
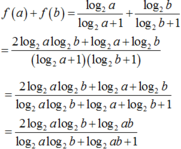
Cần chọn hai giá trị a, b sao cho tử rút gọn được với mẫu.
Ta thường chọn a + b = k hoặc a b = k . Ở bài toán này ta chọn a b = k .
Nếu a b = 1 4 thì log 2 a b = log 2 1 4 = - 2 .
Suy ra
Vậy với các giá trị a, b thỏa mãn a b = 1 4 thì f ( a ) + f ( b ) = 2 .
Ta có
H
4 tháng 4 2017
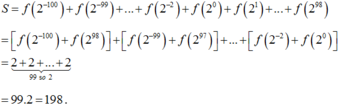
Có:
\(D=2+2^2+2^3+2^4+...+2^{99}+2^{100}\)
\(\Rightarrow2D=2^2+2^3+2^4+2^5+...+2^{100}+2^{101}\)
\(\Rightarrow2D-D=D=2+2^{101}\)
Chúc bạn học tốt!
25 tháng 6 2017
\(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{99}+\sqrt{100}}\)
= \(\dfrac{\sqrt{1}-\sqrt{2}}{-1}+\dfrac{\sqrt{2}-\sqrt{3}}{-1}+...+\dfrac{\sqrt{99}-\sqrt{100}}{-1}\)
= \(\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}+...+\sqrt{100}-\sqrt{99}\)
= \(-\sqrt{1}+\sqrt{100}\) = \(-1+10\) = \(9\)
AH
Akai Haruma
Giáo viên
8 tháng 2 2017
Câu 2)
Đặt \(\left\{\begin{matrix} u=\ln ^2x\\ dv=x^2dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=2\frac{\ln x}{x}dx\\ v=\frac{x^3}{3}\end{matrix}\right.\Rightarrow I=\frac{x^3}{3}\ln ^2x-\frac{2}{3}\int x^2\ln xdx\)
Đặt \(\left\{\begin{matrix} k=\ln x\\ dt=x^2dx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} dk=\frac{dx}{x}\\ t=\frac{x^3}{3}\end{matrix}\right.\Rightarrow \int x^2\ln xdx=\frac{x^3\ln x}{3}-\int \frac{x^2}{3}dx=\frac{x^3\ln x}{3}-\frac{x^3}{9}+c\)
Do đó \(I=\frac{x^3\ln^2x}{3}-\frac{2}{9}x^3\ln x+\frac{2}{27}x^3+c\)
AH
Akai Haruma
Giáo viên
8 tháng 2 2017
Câu 3:
\(I=\int\frac{2}{\cos 2x-7}dx=-\int\frac{2}{2\sin^2x+6}dx=-\int\frac{dx}{\sin^2x+3}\)
Đặt \(t=\tan\frac{x}{2}\Rightarrow \left\{\begin{matrix} \sin x=\frac{2t}{t^2+1}\\ dx=\frac{2dt}{t^2+1}\end{matrix}\right.\)
\(\Rightarrow I=-\int \frac{2dt}{(t^2+1)\left ( \frac{4t^2}{(t^2+1)^2}+3 \right )}=-\int\frac{2(t^2+1)dt}{3t^4+10t^2+3}=-\int \frac{2d\left ( t-\frac{1}{t} \right )}{3\left ( t-\frac{1}{t} \right )^2+16}=\int\frac{2dk}{3k^2+16}\)
Đặt \(k=\frac{4}{\sqrt{3}}\tan v\). Đến đây dễ dàng suy ra \(I=\frac{-1}{2\sqrt{3}}v+c\)
NT
1
10 tháng 9 2017
Xét A = 1 + 2 + 22 + ... + 2100
=> 2A = 2 + 22 + ... + 2101
=> A = 2101 - 2
Do 2101 - 2 < 2101 nên A < B
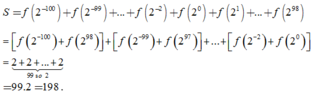
S = 12 + 22 + 32 + ... + 992 + 1002
= 1.1 + 2.2 + 3.3 + ... + 99.99 + 100.100
= 1.(2 - 1) + 2.(3 - 1) + 3.(4 - 1) + ... + 99(100 - 1) + 100.(101 - 1)
= (1.2 + 2.3 + 3.4 + ... + 99.100 + 100.101) - (1 + 2 + 3 + ... + 99 + 100)
Đặt A = 1.2 + 2.3 + 3.4 + ... + 99.100 + 100.101
3A = 1.2.3 + 2.3.3 + 3.4.3 + .... + 99.100.3 + 100.101.3
= 1.2.3 + 2.3.(4 - 1) + 3.4.(5 - 2) + .... + 99.100.(101 - 98) + 100.101.(102 - 99)
= 1.2.3 + 2.3.4 - 1.2.3 + 3.4.5 - 2.3.4 + ... + 99.100.101 - 98.99.100 + 100.101.102 - 99.101.102
= 100.101.102
=> A = 100.101.102 : 3 = 343400
Khi đó S = 343400 - (1 + 2 + 3 + 4 + ... + 100)
= 343400 - 100.(100 + 1) : 2
= 343400 - 5050 = 338 350
Vậy S = 338350
bạn ơi sao bạn còn đi trả lời câu hỏi này cho người khác mà bạn còn đi hỏi hài nay làm gì vậy