Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện xác định: \(x^2-2x+1>0\)
Mà \(x^2-2x+1=\left(x-1\right)^2\ge0\forall x\in R\)
\(\Rightarrow x-1\ne0\\ \Leftrightarrow x\ne1\)
Vậy D = \(R/\left\{1\right\}\) ⇒ Chọn B.

Hàm số xác định khi: \(\sin x - 1\; \ne 0\; \Leftrightarrow \sin x \ne 1\; \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi ,\;\;k \in \mathbb{Z}\)
Vậy ta chọn đáp án B

Hàm số \(x^{-3}\) xác định \(\Leftrightarrow x\ne0\)
\(\Rightarrow C\)

Hàm số \(x^{\dfrac{3}{5}}\) xác định \(\Leftrightarrow x>0\)
\(\Rightarrow D\)

Đồ thị này cắt trục Ox tại rất nhiều điểm chứ không phải chỉ có 1 điểm
=>Chọn C

Hàm xác định trên R khi với mọi x ta có:
\(sin^6x+cos^6x+m.sinx.cosx>0\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x+\dfrac{m}{2}sin2x>0\)
\(\Leftrightarrow3sin^22x-2m.sin2x-4< 0\)
Đặt \(sin2x=t\in\left[-1;1\right]\Rightarrow3t^2-2mt-4< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}3.f\left(-1\right)< 0\\3.f\left(1\right)< 0\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2m-1< 0\\-2m-1< 0\end{matrix}\right.\)
\(\Rightarrow-\dfrac{1}{2}< m< \dfrac{1}{2}\)

Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C

\(y=\dfrac{cotx}{cosx-1}\)
Đk:\(cosx-1\ne0\Leftrightarrow cosx\ne1\)\(\Leftrightarrow x\ne k\pi,k\in Z\)
\(D=R\backslash\left\{k\pi;k\in Z\right\}\)
Ý C
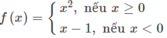
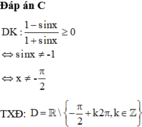
ĐKXĐ.: x ≥ 0
TXĐ: D = 0 ; + ∞
Chọn đáp án C.