Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: TXĐ: \(D=R\backslash\left\{-\dfrac{1}{2}\right\}\)
b: TXĐ: \(D=R\backslash\left\{-3;1\right\}\)
c: TXĐ: \(D=\left[-\dfrac{1}{2};3\right]\)

b: A là tập con của B
A là tập con của C
A là tập con của D và ngược lại

a) Phương trình \({x^2} - 2 = 0\) có hai nghiệm là \(\sqrt 2 \) và \( - \sqrt 2 \), nên \(A = \{ \sqrt 2 ; - \sqrt 2 \} \)
Tập hợp \(B = \{ x \in \mathbb{R}|2x - 1 < 0\} \) là tập hợp các số thực \(x < \frac{1}{2}\)
Từ đó \(A \cap B = \{ - \sqrt 2 \} .\)
b) \(A \cap B = \{ (x;y)|\;x,y \in \mathbb{R},y = 2x - 1,y = - x + 5\} \)
Tức là \(A \cap B\)là tập hợp các cặp số (x; y) thỏa mãn hệ phương trình: \(\left\{ \begin{array}{l}y = 2x - 1\\y = - x + 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}2x - 1 = - x + 5\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\y = 2x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right.\)
Vậy \(A \cap B = \{ (2;3)\} .\)
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
\(A \cap B\) là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi.
Một tứ giác bất kì thuộc \(A \cap B\) thì nó là hình chữ nhật và có 2 cạnh kề bằng nhau (hình vuông)
Do đó \(A \cap B\) là tập hợp các hình vuông.

a) \(A=\left\{x\in R|x-\sqrt[]{3-2x}=0\right\}\)
\(B=\left\{x\in R|x^2+2x-3=0\right\}\)
\(\)\(x-\sqrt[]{3-2x}=0\)
\(\Leftrightarrow\sqrt[]{3-2x}=x\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\3-2x=x^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2+2x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow x=1\)
\(\Rightarrow A=\left\{1\right\}\)
\(x^2+2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
\(\Rightarrow B=\left\{-3;1\right\}\)
Vậy \(A\subset B\)
b) \(A=\left\{x\in N|x^2-2x+1>10\right\}\)
\(B=\left\{x\in N|x>=2\right\}\)
\(x^2-2x+1>10\)
\(\Leftrightarrow\left(x-1\right)^2>\left(\sqrt[]{10}\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< -\sqrt[]{10}\\x-1>\sqrt[]{10}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1-\sqrt[]{10}\\x>1+\sqrt[]{10}\end{matrix}\right.\)
\(\Rightarrow A=(-\infty;1-\sqrt[]{10})\cup(1+\sqrt[]{10};+\infty)\)
\(B=[2;+\infty)\)
mà \(1-\sqrt[]{10}< 2< 1+\sqrt[]{10}\)
Vậy 2 tập hợp không có quan hệ gì giữa nhau

3x-1>=2 và 3-x>1
=>x<2 và 3x>=3
=>1<=x<2
=>A=[1;2)
B=[0;3]
\(C_BA=B\text{A}=\left[2;3\right]\)
=>Chọn B

\(A=\left\{x\in R|-2\le x\le2\right\}\)
\(B=\left\{x\in R|x\ge3\right\}\)
\(C=\left(-\infty;0\right)\)
\(A\cup B=\left[-2;2\right]\cup[3;+\infty)\)
\(A\)\\(C=\left[0;2\right]\)
\(A\cap B=\varnothing\)
\(B\cap C=\varnothing\)

a) \(A \cup B = \{ a;b;c;d;e;i;u\} \), \(A \cap B = \{ a;e\} \)
b) Phương trình \({x^2} + 2x - 3 = 0\) có hai nghiệm là 1 và -3, nên \(A = \{ 1; - 3\} \)
Phương trình \(B = \{ x \in \mathbb{R}|\;|x|\; = 1\} \) có hai nghiệm là 1 và -1, nên \(B = \{ 1; - 1\} \)
Từ đó, \(A \cup B = \{ 1; - 1; - 3\} \), \(A \cap B = \{ 1\} .\)

Bài 4: B
Bài 5:
a: {3;5};{3;7};{5;7};{3;5;7};{3};{5};{7};\(\varnothing\)

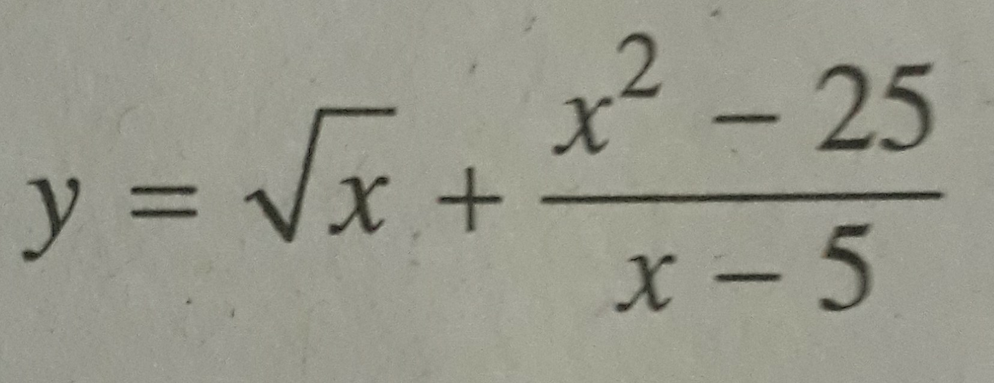
Đáp án A