Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
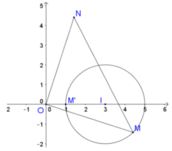
Gọi z 1 = x + y i ; x , y ∈ ℝ .
Khi đó điểm biểu diễn số phức z 1 là M(x;y) thỏa mãn.
Do đó tập hợp các điểm biểu diễn số phức z 1
là đường tròn tâm I(3;0) bán kính R = 2
Ta có z 2 = i z 1 = i x + y i = - y + i x .
Khi đó tam giác MON vuông cân tại O.
M N = O M 2 nên MN nhỏ nhất
Û OM nhỏ nhất
Û M ≡ M ' (M’ là giao điểm của OI với đường tròn
về phía bên trái như hình vẽ).
Tức là M(1;0). Khi đó M N = 2 O M = 2 . 1 = 2

Ta có : w - 1 + 2 i = z ⇔ w = z + 1 - 2 i . Suy ra quỹ tích các điểm biểu diễn số phức w có được từ quỹ tích các điểm biểu diễn số phức z bằng cách thực hiện phép tịnh tiến theo v → = ( 1 ; - 2 ) . Do đó quỹ tích quỹ tích các điểm biểu diễn số phức w là đường tròn tâm (-1;1) bán kính bằng 3.
Đáp án D
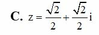



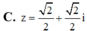



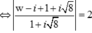

Chọn C
Gọi M(a; b) là điểm biểu diễn số phức A(-1,1), R = 1
Ta có:
Khi đó, số phức z = i và M(0;1)
Vì a2 + b2 = 1 nên điểm M biểu diễn số phức z thuộc đường tròn tâm O(0;0), bán kính R = 1
Vì điểm M(0; 1) nên M thuộc đường thẳng y = 1.
Tập hợp các điểm biểu diễn là giao điểm của đường tròn tâm O, bán kính R = 1 và đường thẳng y = 1.