
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn 5 cuốn bất kì từ 16 cuốn và tặng cho 5 em: có \(C_{16}^5=4368\) cách
TH1: trong 5 cuốn sách chỉ có đúng 1 loại sách (5 cuốn toàn toán hoặc toán hóa): \(C_5^5+C_7^5=22\) cách
TH2: 5 cuốn chỉ có đúng 2 loại toán và lý: \(C_9^5-C_5^5=125\) cách
TH3: 5 cuốn chỉ có đúng 2 loại toán và hóa: \(C_{12}^5-\left(C_5^5+C_7^5\right)=770\)
TH4: 5 cuốn chỉ có đúng 2 loại lý và hóa: \(C_{11}^5-C_7^5=441\) cách
\(\Rightarrow\) Số cách để chọn 5 cuốn có đủ loại sách là:
\(4368-\left(22+125+770+441\right)=3010\) (cách)
Đem 5 cuốn đó tặng cho 5 em: có \(3010.5!=...\) cách

Tham khảo:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Tổng số giờ làm không quá 10 giờ nên \(2x + y \le 10\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + y \le 10\\x \ge 0\\y \ge 0\end{array} \right.(x,y \in \mathbb{N})\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
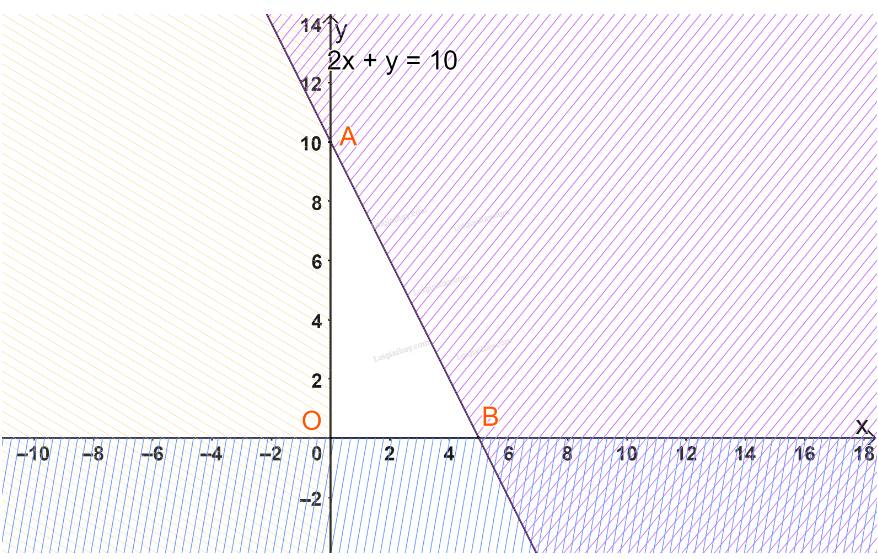
Miền không gạch chéo (miền tam giác OAB, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.

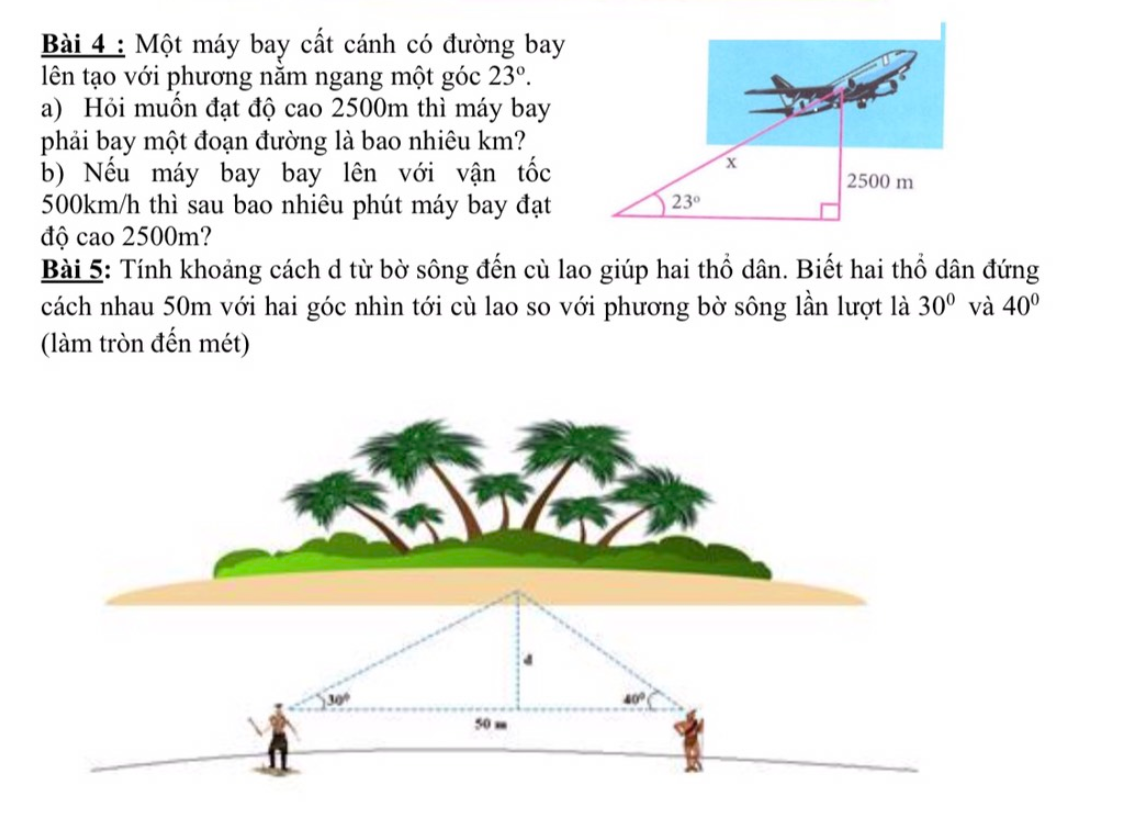
Bài 4:
a) Gọi AB là độ cao máy bay, BC là đoạn đường máy bay bay
Áp dụng tslg trong tam giác ABC vuông tại A:
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{2500}{sin23^0}\approx6398\left(m\right)\)
b) Đổi: \(6398m=6,398km\)
Thời gian máy bay đạt độ cao 2500m:
\(t=\dfrac{S}{v}=\dfrac{6,398}{500}\approx0,03h=1,8ph\)







Cả lớp mình đi làm lễ 20/11 nà^^!
ukm