Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

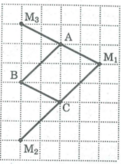
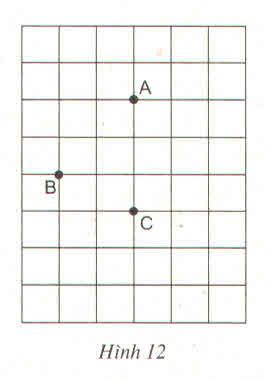
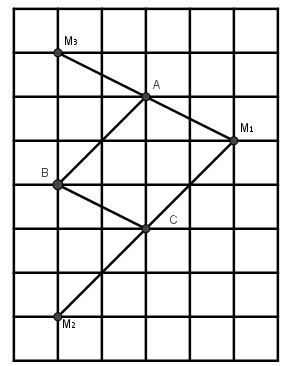
- Nếu hình bình hành nhận AC làm đường chéo vì AB là đường chéo hình vuông có 2 ô vuông nên C M 1 là đường chéo hình vuông cạnh 2 ô vuông và A, M 1 nằm trên một nửa mặt phẳng bờ BC ta có hình bình hành ABC M 1
- Nếu hình bình hành nhận BC làm đường chéo, điểm A cách điểm C ba ô vuông, điểm B cách điểm M 2 là ba ô vuông và trên một nửa mặt phẳng bờ AB ta có hình bình hành AB M 2 C
- Nếu hình bình hành nhận AB làm đường chéo thì điểm M 3 cách điểm B ba ô vuông, M 3 và A nằm trên cùng một nửa mặt phẳng bờ BC ta có hình bình hành ACB M 3

Bài giải:
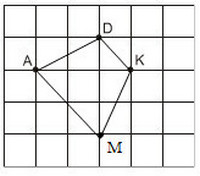
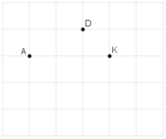
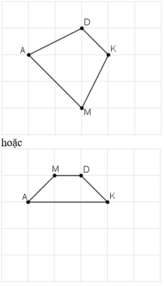
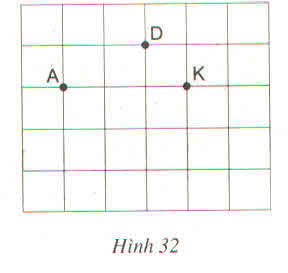
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình thang ADKM2 (với DK là đáy).
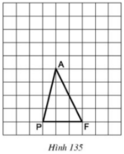
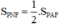
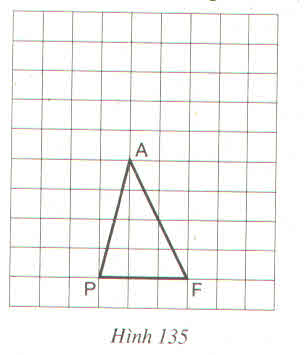
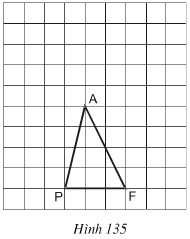


Gọi AH là chiều cao của tam giác APF.
Ta có: SAPF = AH.PF/2.
a) SPIF = SPAF
⇔ chiều cao IK = AH (Chung cạnh đáy PF).
⇔ I nằm trên đường thẳng song song với PF và cách PF 1 khoảng bằng AH.
b) SPOF = 2.SPAF
⇔ chiều cao OM = 2.AH
⇔ O nằm trên đường thẳng song song với PF và cách PF một khoảng bằng 2.AH
c)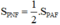
⇔ chiều cao NQ = AH/2
⇔ N nằm trên đường thẳng song song với PF và cách PF một khoảng bằng AH/2.