Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

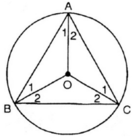
Vì tam giác ABC là tam giác đều nên 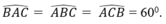
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
![]()
* Xét tam giác AOB có:
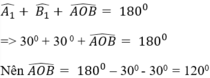
* Tượng tự ta được: ![]()
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)

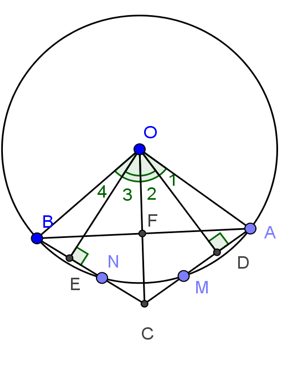
Xét đường tròn tâm (O) có AM=BN
Từ đó ta suy ra OE=OD (tính chất quan hệ giữa đường kính và dây cung)
Xét tam giác vuông AOD và tam giác vuông BOE có:
OA=OB(cùng bằng bán kính)
OE=OD(chứng minh trên)
=> ΔAOD = ΔBOE (cạnh huyền-cạnh góc vuông)
=> ∠O1 = ∠O4 (2 góc tương ứng)(1)
Tương tự ta có: ∠O2 = ∠O3 (2)
Ta có: ∠AOC = ∠O1 + ∠O2
∠BOC = ∠O3 + ∠O4
Từ (1) và (2) ta suy ra ∠AOC= ∠BOC
Suy ra OC là tia phân giác của góc AOB.
Xét tam giác OBF và tam giác OAF có:
∠AOC = ∠BOC (chứng minh trên)
OA=OB
OF: chung
Suy ra ΔOBF = ΔOAF (c-g-c)
=> BF=AF( 2 cạnh tương ứng)
=> OC ⊥ AB
a. Kẻ \(OH\perp AM ; OK\perp AN\)
Ta có: AM = AN ( gt )
Suy ra: OH = OK ( hai dây bằng nhau cách đều tâm )
Xét hai tam giác OCH và OCK, ta có :
\(\widehat{OHC}=\widehat{OKC}=90^o\)
OC chung
OH = OK (chứng minh trên)
Suy ra: \(\Delta OIH=\Delta OIK\)( cạnh huyền, cạnh góc vuông )
Xét hai tam giác OAH và OBH, ta có :
\(\widehat{OHA}=\widehat{OHB}=90^o\)
OA = OB
OH = OK (chứng minh trên)
Suy ra: \(\Delta OAH=\Delta OBH\)( cạnh huyền, cạnh góc vuông )
\(\widehat{O_3}=\widehat{O_4}\)
Suy ra : \(\widehat{O_1}+\widehat{O_3}=\widehat{O_2}+\widehat{O_4}\)hay \(\widehat{AOC}=\widehat{BOC}\)
Vậy OC là tia phân giác của \(\widehat{AOB}\)
b. Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân )
Suy ra: \(OC\perp AB\)

Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được