Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài làm
Gọi giao điểm của đường trung trực BC và HC là I.
=> NI vuông góc BC
Mà AH vuông góc BC
=> NI // AH
Ta có: BC = BH + HC
hay BC = 15 + 27
=> BC = 42
Mà I là trung điểm BC ( Do IN trung trực )
=> BI = IC = 42/2 = 21 ( cm )
Xét tam giác AHC có:
IN // AH
Theo định lí Thales có:
\(\frac{IC}{HC}=\frac{CN}{AC}\)
hay \(\frac{21}{27}=\frac{CN}{45}\)
=> CN = 21 . 45 / 27 = 35
Vậy CN = 35 cm
# Học tốt #
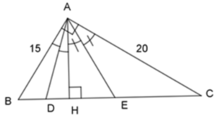
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
A B 2 + A C 2 = B C 2 ⇔ 15 2 + 20 2 = B C 2 ⇒ B C = 25
Ta có: S A B C = 1 2 .AB.AC = 1 2 .AH.BC ⇒ A H = A B . A C B C = 15.20 25 = 12
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
A B 2 = A H 2 + H B 2 ⇔ 15 2 = 12 2 + H B 2 ⇒ H B 2 = 81 ⇒ H B = 9 ⇒ H C = B C – H B = 25 – 9 = 16
Vì AE là phân giác của tam giác CAH nên: A C A H = C E E H ⇔ A C A H = C H − H E E H
ó 20 12 = − H E H E ó 20HE = 12(16 – HE) ó 20HE + 12HE = 12.16
ó 32HE = 192 ó HE = 6(cm)
Đáp án: B
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
A B 2 + A C 2 = B C 2 ⇔ 15 2 + 20 2 = B C 2 ⇒ B C = 25
Ta có: S A B C = 1 2 .AB.AC = 1 2 .AH.BC ⇒ A H = A B . A C B C = 15.20 25 = 12
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
A B 2 = A H 2 + H B 2 ⇔ 15 2 = 12 2 + H B 2 ⇒ H B 2 = 81 = > H B = 9 ⇒ H C = B C – H B = 25 – 9 = 16
Vì AD là phân giác của tam giác ABH nên: A B A H = B D D H ⇔ A B A H = B H − D H D H
⇔ 15 12 = 9 − D H D H ó 15DH = 108 – 12DH ó DH = 4cm
Đáp án: A