
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do tam giác ABC đều nên tâm đường tròn ngoại tiếp O trùng trọng tâm
Gọi AM là trung tuyến (kiêm đường cao), theo tính chất trọng tâm:
\(AM=\dfrac{3}{2}AO=\dfrac{3}{2}R=12\)
\(AM=\dfrac{AB\sqrt{3}}{2}\Rightarrow AB=8\sqrt{3}\)
\(S=\dfrac{1}{2}AM.AB=48\sqrt{3}\)
Tam giác ABC đều.
\(\Rightarrow AB=AC=BC\) (Tính chất tam giác đều).
Áp dụng định lý sin vào tam giác ABC đều, ta có:
\(\dfrac{a}{\sin A}=2R.\Rightarrow\dfrac{BC}{\sin60}=2.8.\Leftrightarrow BC=16.\dfrac{\sqrt{3}}{2}=8\sqrt{3}\) (đvđd).
\(\Rightarrow BC^2=192\) (đvđd).
Ta có: \(S=\dfrac{1}{2}ac.\sin B.\)
\(\Rightarrow S=\dfrac{1}{2}BC.AB.\sin60^o=\dfrac{1}{2}.BC^2.\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{3}}{4}.192=48\sqrt{3}\) (đvdt).

Nhận xét: Tam giác ABC có a2 + b2 = c2 nên vuông tại C.
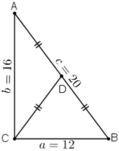
+ Diện tích tam giác: S = 1/2.a.b = 1/2.12.16 = 96 (đvdt)
+ Chiều cao ha: ha = AC = b = 16.
+ Tâm đường tròn ngoại tiếp tam giác là trung điểm của AB.
Bán kính đường tròn ngoại tiếp R = AB /2 = c/2 = 10.
+ Bán kính đường tròn nội tiếp tam giác: S = p.r ⇒ r = S/p.
Mà S = 96, p = (a + b + c) / 2 = 24 ⇒ r = 4.
+ Đường trung tuyến ma:
ma2 = (2.(b2 + c2) – a2) / 4 = 292 ⇒ ma = √292.

Gọi O là tâm đa giác, giả sử A, B là hai đỉnh kề nhau của đa giác
Ta có A O B ^ = 360 n ° . Diện tích đa giác đều bằng.
S = n S O A B = n . 1 2 O A . O B . sin A O B ^ = 1 2 n R 2 . sin 360 n °
ĐÁP ÁN A

Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)

\(\widehat{A}=180^o-30^o-44^o=106^o.\)
Áp dụng định lý sin ta có:
\(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}=\dfrac{AB}{sinC}.\)
\(\Rightarrow\dfrac{BC}{sin106^o}=\dfrac{7}{sin44^o}=\dfrac{AB}{sin30^o}.\)
\(\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{7.sin106^o}{sin44^o}\approx9,7.\\AB=\dfrac{7.sin30^o}{sin44^o}\approx5,0.\end{matrix}\right.\) (đvđd).
\(S_{\Delta ABC}=\dfrac{1}{2}AB.AC.\sin A\approx\dfrac{1}{2}.5,0.7.\sin106^o\approx17,4\) (đvdt).
\(S=pr=\dfrac{AB+AC+BC}{2}.r.\\ \Rightarrow17,4\approx\dfrac{5,0+7+9,7}{2}.r.\)
\(\Rightarrow r\approx1,6\) (đvđd).
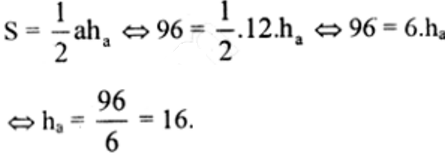
Xét \(\Delta\)ABC đều, có độ dài cạnh bằng a
Theo định lý sin ta có: \(\frac{BC}{\sin\widehat{BAC}}=2R\Leftrightarrow\frac{a}{\sin60^o}=2\cdot4\Leftrightarrow a=8\cdot\widehat{60^o}=4\sqrt{3}\)
Vậy diện tích tam giác cần tính là: \(S_{\Delta ABC}=\frac{1}{2}AB\cdot AC\cdot\sin\widehat{BAC}=\sin\left(4\sqrt{3}\right)^2\cdot\sin60^o=12\sqrt{3}\left(cm^2\right)\)
Nguồn: Hoàng Ngọc Khánh