
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



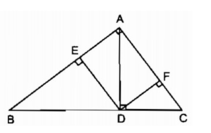
DE và CA cùng vuông góc với AB, do đó
DE // AC.
Theo định lí Ta-lét, ta có:
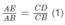
Tương tự, ta có: DF // AB, do đó:
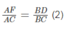
Cộng các vế tương ứng của (1) và (2), ta có:
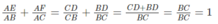
Tổng 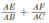 không thay đổi vì luôn có giá trị bằng 1.
không thay đổi vì luôn có giá trị bằng 1.
Vậy : Khi độ dài cạnh góc vuông AB, AC của tam giác vuông ABC thay đổi thì tổng 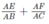 luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.
luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.

Hình pạn tự vẽ nha!!!
Bài Làm:
Xét \(\Delta ABC\) có \(DE//AC\left(gt\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{CD}{CB}\left(1\right)\) ( Theo định lí Ta - lét )
Lại có: \(DF//AB\left(gt\right)\)
\(\Rightarrow\dfrac{AF}{AC}=\dfrac{BD}{CB}\left(2\right)\) ( Theo định lí Ta - lét )
Từ (1) và (2) \(\Rightarrow\) \(\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{CD}{CB}+\dfrac{BD}{CB}\)
\(\Leftrightarrow\dfrac{AE}{AB}+\dfrac{AF}{AC}=\dfrac{CD+DB}{CB}=\dfrac{CB}{CB}=1\)
Chúc pạn hok tốt!!!

a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
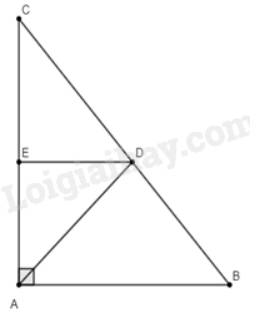
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2

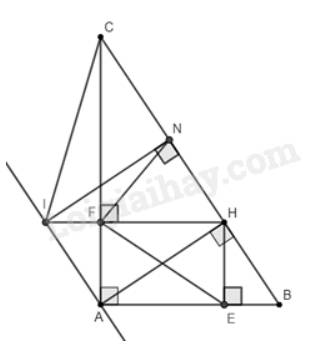
a) Vì \(AH\) là đường cao nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)
Xét tam giác \(ABH\) và tam giác \(CBA\) có:
\(\widehat B\) (chung)
\(\widehat {AHB} = \widehat {CAB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta ABH\backsim\Delta CBA\) (g.g).
Do đó, \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{B^2} = BH.BC\) .
b)
- Vì \(HE\) vuông góc với \(AB\) nên \(\widehat {HEA} = \widehat {HEB} = 90^\circ \)
Xét tam giác \(AHE\) và tam giác \(ABH\) có:
\(\widehat {HAE}\) (chung)
\(\widehat {HEA} = \widehat {AHB} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHE\backsim\Delta ABH\) (g.g).
Do đó, \(\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{H^2} = AB.AE\) . (1)
- Vì \(HF\) vuông góc với \(AC\) nên \(\widehat {HFC} = \widehat {HFA} = 90^\circ \)
Xét tam giác \(AHF\) và tam giác \(ACH\) có:
\(\widehat {HAF}\) (chung)
\(\widehat {AFH} = \widehat {AHC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AHF\backsim\Delta ACH\) (g.g).
Do đó, \(\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(A{H^2} = AF.AC\) . (2)
Từ (1) và (2) suy ra, \(AE.AB = AF.AC\) (điều phải chứng minh)
c) Vì \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).
Xét tam giác \(AFE\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (chứng minh trên)
Suy ra, \(\Delta AFE\backsim\Delta ABC\) (c.g.c).
d) Vì \(HF\) vuông góc với \(AC\) nên \(CF \bot HI\), do đó, \(\widehat {CFH} = \widehat {CFI} = 90^\circ \).
Vì \(IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ \).
Xét tam giác \(HFC\) và tam giác \(HNI\) có:
\(\widehat {CHI}\) (chung)
\(\widehat {HFC} = \widehat {HNI} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta HFC\backsim\Delta HNI\) (g.g).
Suy ra, \(\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}\) (hai cặp cạnh tương ứng cùng tỉ lệ)
Do đó, \(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\).
Xét tam giác \(HNF\) và tam giác \(HIC\) có:
\(\widehat {CHI}\) (chung)
\(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\) (chứng minh trên)
Suy ra, \(\Delta HNF\backsim\Delta HIC\) (c.g.c).

a) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{DB}{DC}=\dfrac{6}{8}=\dfrac{3}{4}\)