Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A. \(\sin A = \sin \,(B + C)\)
Ta có: \((\widehat A + \widehat C) + \widehat B= {180^o}\)
\(\Rightarrow \sin \,(B + C) = \sin A\)
=> A đúng.
B. \(\cos A = \cos \,(B + C)\)
Sai vì \(\cos \,(B + C) = - \cos A\)
C. \(\;\cos A > 0\) Không đủ dữ kiện để kết luận.
Nếu \({0^o} < \widehat A < {90^o}\) thì \(\cos A > 0\)
Nếu \({90^o} < \widehat A < {180^o}\) thì \(\cos A < 0\)
D. \(\sin A\,\, \le 0\)
Ta có \(S = \frac{1}{2}bc.\sin A > 0\). Mà \(b,c > 0\)
\( \Rightarrow \sin A > 0\)
=> D sai.
Chọn A

A. \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\) (Loại)
Vì: Theo định lí cos ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
Không đủ dữ kiện để suy ra \({a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)
B. \(\frac{b}{{\sin A}} = \frac{a}{{\sin B}}\) (Loại)
Theo định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \nRightarrow \frac{b}{{\sin A}} = \frac{a}{{\sin B}}\)
C. \(\sin B = \frac{{ - \sqrt 2 }}{2}\)(sai vì theo câu a, \(\sin B = \frac{{\sqrt 2 }}{2}\))
D. \({b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)
Theo định lý cos ta có:
\({b^2} = {c^2} + {a^2} - 2ca.\cos B\) (*)
Mà \(\widehat B = {135^o} \Rightarrow \cos B = \cos {135^o}\).
Thay vào (*) ta được: \({b^2} = {c^2} + {a^2} - 2ca\;\cos {135^o}\)
=> D đúng.
Chọn D

Theo đl sin có:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow b=a\dfrac{sinB}{sinA};c=\dfrac{sinC}{sinA}.a\)
Mà `b+c=2a`
\(\Rightarrow a\dfrac{sinB}{sinA}+a\dfrac{sinC}{sinA}=2a\\ \Rightarrow\dfrac{sinB}{sinA}+\dfrac{sinC}{sinA}=2\\ \Leftrightarrow sinB+sinC=2sinA\)
Chọn B

1) \(sin\left(A+2B+C\right)=sin\left(\pi-B+2B\right)\)
=\(sin\left(\pi+B\right)=sin\left(-B\right)=-sinB\)
2) \(sinBsinC-cosBcosC=-cos\left(B+C\right)\)
\(=-cos\left(\pi-A\right)=cosA\)
4) bạn ơi +2 vào vế phải mới đúng nhé
2+ \(2cosAcosBcosC=\left[cos\left(A+B\right)+cos\left(A-B\right)\right]cosC+2\)
\(=cos\left(\pi-C\right)cosC+cos\left(A-B\right)cos\left(\pi-\left(A+B\right)\right)+2\)
=\(-cos^2C-cos\left(A-B\right)cos\left(A+B\right)+2\)
\(=-cos^2C-\frac{1}{2}\left(cos2A+cos2B\right)+2\)
\(=-cos^2C-\frac{1}{2}\left(2cos^2A-1\right)-\frac{1}{2}\left(2cos^2B-1\right)+2\)
\(=-cos^2C-cos^2A+\frac{1}{2}-cos^2C+\frac{1}{2}+2\)
= sin2C - 1 + sin2A - 1 + sin2C - 1 + 3
= sin2A + sin2B + sin2C

Chọn B.
Ta có: góc A tù nên cos A < 0 ; sinA > 0 ; tan A < 0 ; cot A < 0
Do góc A tù nên góc B và C là các góc nhọn có các giá trị lượng giác đều dương
Do đó: M > 0 ; N > 0 ; P > 0 và Q < 0.

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
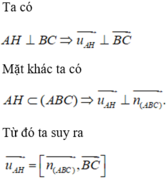
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.
Ta có; cosB =cos 30 0 = 3 2 ⇒ sin C = c osB = 3 2
Và sinB =sin 30 0 = 1 2 ⇒ c os C = sinB = 1 2
Chọn A.